Using the variance function g(h) created via the variogram, the interpolation weights λ_i(x, y) are now defined for an interpolation point (x, y) in such a way that the following moving average equation applies:

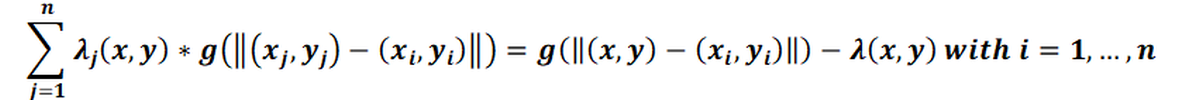
with

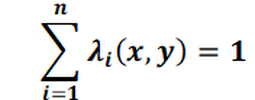
This leads to a ((n+1) x (n+1)) dimensional system of equations for the weights λ_i(x, y), i=1,...,n

and the parameter g(x, y):

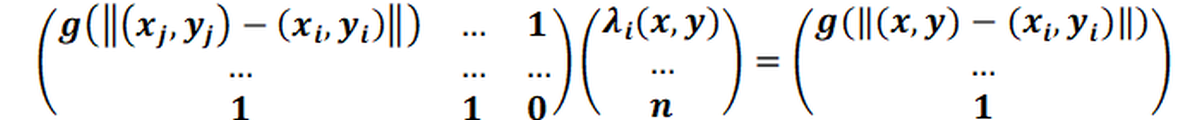
The matrix of the system of equations is independent of the interpolation point (x, y). During interpolation, an LU decomposition of this matrix is carried out. For each interpolation point (x, y), the system of equations for the interpolation weights can then be solved by simply solving back to the corresponding right-hand side. For each interpolation point, the variance:

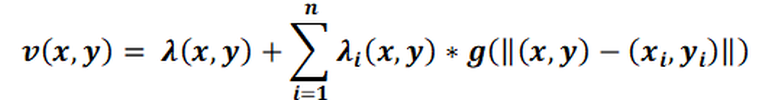
is calculated. This value must be 0 for all interpolation points. If this is not the case for some points, this indicates numerical problems or rounding errors in the kriging interpolation. The number of points with v < 0 is then output as a warning.

Input parameters for Kriging