The following additional options appears in the input window:

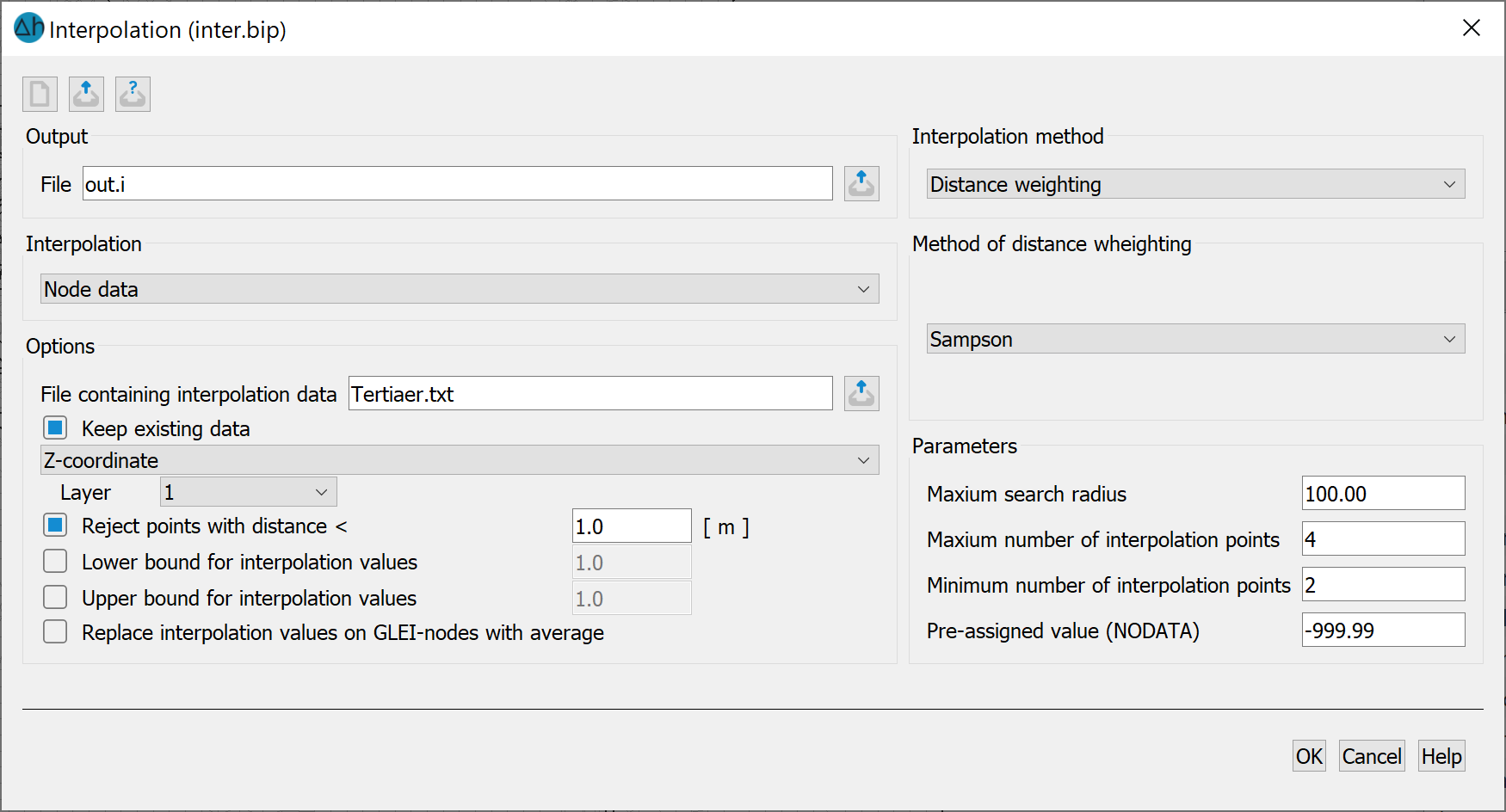
Inputs for the distance weighting

 

The available interpolation data is weighted according to its distance d from the node or element centre point being searched for. Four methods can be selected for the weighting:

• Sampson (see in the following),

• Linear (1/d),

• Quadratic (1/d²),

• 4th order (1/d⁴),

 

where d is the distance from the interpolation point to the interpolation point.

 

The user determines the maximum search radius in which measuring points are searched for as well as the maximum and minimum number of interpolation points to be included in the interpolation. If no interpolation point or too few interpolation points are found within the specified search radius, no value is interpolated for the node or element in question and instead the node or element value is set to a pre-assigned value (No data or default value) defined by the user.

 

Note: When interpolating data using the Attributes Assign By interpolation... menu item, nodes or elements for which not enough interpolation points were found do not receive a value!

In the linear case, the influence of a data point on the interpolation point decreases linearly with distance, which generally leads to a relatively rough interpolation surface with approximately linear transitions between the data points. With 4th order weighting, the influence of a point decreases with the fourth power of its distance, so that the value of the nearest point is of very great importance. This method produces very smooth, but slightly stepped surfaces around the data points. Quadratic weighting mediates between these two extremes.

The method according to Sampson (1978) was also published under the name "inverse distance-squared weighting" and is based on the following weighting function:

 

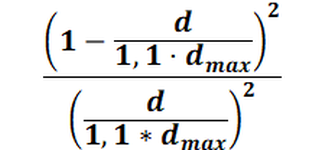
Of the four weighting methods listed, this method generally provides the most favourable results.

 

 

Kriging