Durch Aktivieren der Schaltfläche „Erweitert“ lassen sich weitere Parameter festlegen. Zunächst werden die Eingaben des Moduls SITRA beschrieben:

 

 

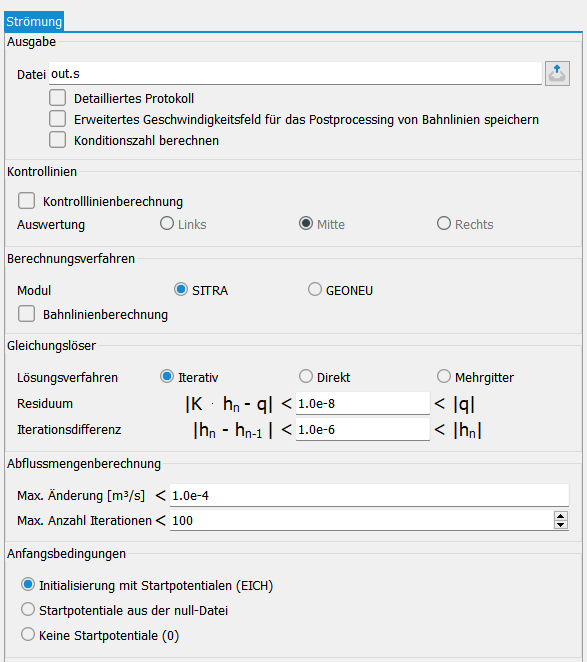
Ausgabe

Hier wird der Name der Ausgabedatei festgelegt. Voreingestellt ist der Name out.s im Modul SITRA bzw. out.g im Modul GEONEU.

Bei einem detaillierten Protokoll (nur SITRA) werden neben den Zwischenzeitpunkten einer instationären Rechnung auch die Massenbilanzen (knotenweise) und eventuell berechnete Kontrolllinienmengen (knotenweise), berechnete Potentiale, Konzentrationen bzw. Temperaturen, Sättigungen (bei gesättigt/ungesättigter Rechnung) und Geschwindigkeiten protokolliert.

 

 

Erweitertes Geschwindigkeitsfeld für das Postprocessing von Bahnlinien speichern

Bei Aktivierung dieses Kontrollkästchen werden während der stationären Berechnung mit SITRA zusätzliche Geschwindigkeitsvektoren gespeichert. Im 2D erfolgt dies an den Elementkanten sowie in den in Subdreiecke zerlegten Elementen. Im 3D werden die Vektoren an den Gauss-Punkten der Elemente gespeichert.

Nach der Strömungsberechnung steht dann im Menü Datei Exportieren... die Schaltfläche Bahnlinien

zur Verfügung (vgl. Datenexport: Ausgabe von Bahnlinien). Wird das erweiterte Geschwindigkeitsfeld gespeichert, lassen sich Bahnlinienplots nach einer Strömungsberechnung beliebig verändern (vgl. Ploterstellung (Bahnlinien).

 

Konditionszahl berechnen

Bei Aktivierung wird in jedem Zeitschritt die Konditionszahl der Matrix des Gleichungssystems der Strömung berechnet. Sie ist ein Maß für die Stabilität des Problems sowie des Lösungsverfahrens und wird als das Verhältnis zwischen dem kleinsten und größten Eigenwert der Koeffizientenmatrix definiert. Eine niedrige Konditionszahl weist auf ein gutgestelltes Gleichungssystem mit guten Konvergenzeigenschaften hin. Dabei hat ein perfektes Gleichungssystem eine Konditionszahl von 1. Bei einer instationären Strömung wird die Konditionszahl in jedem Zeitschritt berechnet und ausgegeben.

 

Kontrolllinien

(nur wenn Attribut KONT in der Modelldatei vorhanden ist)

Nach Aktivieren des Kontrollkästchens wird die Berechnung der Kontrolllinien durchgeführt. Die Auswertung erfolgt wahlweise über die Geschwindigkeit des linken oder rechten anliegenden Elements oder durch Mittelung der beiden Geschwindigkeiten.

 

Berechnungsverfahren

Es stehen die zwei Berechnungsmodule SITRA und GEONEU zur Verfügung. Voreingestellt ist eine Berechnung mit dem Modul SITRA. Zudem wird ausgewählt, ob Bahnlinien berechnet werden. Der Bahnlinien-Dialog wird im How To - Einzugsgebiete beschrieben.

 

Gleichungslöser

Als Gleichungslöser kann entweder der iterative PCG-Löser, der direkte Cholesky-Gleichungslöser (LU-Zerlegung) oder ein algebraischer Mehrgitter-Gleichungslöser gewählt werden. Wegen seiner Rechenzeit- und Speicherplatzvorteile empfiehlt sich ab ca. 500 Knoten der iterative Gleichungslöser. Im Gegensatz zum direkten Verfahren wird die Lösung zwar nicht exakt berechnet, aber der Fehler ist in der Regel vernachlässigbar gering. Eine Genauigkeitsprüfung kann anhand der in der Ausgabedatei angegebenen Massenbilanz erfolgen. Der Mehrgitter-Gleichungslöser empfiehlt sich vor allem bei Modellen mit großen lokalen Unterschieden in den Durchlässigkeiten.

 

• iterativer PCG-Löser: Allgemeines CG-Verfahren mit Vorkonditionierung (Preconditioned Conjugate Gradient Solver) mit Block-SSOR-Relaxation (Symmetric Successive Over Relaxation Method)

• direkter Gleichungslöser: Gauß-Eliminationsverfahren

• Mehrgitter-Gleichungslöser: CG-Verfahren mit Vorkonditionierung durch Mehrgitterverfahren

 

Residuum und Iterationsdifferenz (nur bei iterativem oder Mehrgitter-Gleichungslöser)

Die Grundlage der iterativen Lösungsverfahren bildet das als Variationsproblem definierte Randwertproblem, aus dem sich durch Diskretisierung eine quadratische Funktion F(v) ergibt, deren Minimum die gesuchte Lösung liefert. Durch partielle Differentiation von F entsteht als notwendige Bedingung für diese Minimierung das bekannte symmetrische und positiv definite Gleichungssystem

K h* = q

Mit:

K = Durchlässigkeit

h* = Lösungsvektor der Potentiale

q = Vektor der Quellen/Senken

 

Mit h* sei im Folgenden der exakte Lösungsvektor bezeichnet, der nun mittels eines iterativen Verfahrens ermittelt werden soll. Mit h als so genanntem Versuchsvektor kann die quadratische Funktion wie folgt geschrieben werden:

 

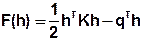
Mit:

h^T = transformierter Versuchsvektor der Potentiale

K = Durchlässigkeitsmatrix

h = Versuchsvektor der Potentiale

q^T = transformierter Vektor der Quellen/Senken

 

 

bzw. in Indexschreibweise:

 

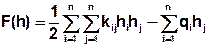
Die partielle Differentiation nach h_i liefert:

 

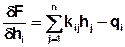
Darin ist δF / δh_i die i-te Komponente des Gradienten oder auch Residuenvektors g für den Versuchsvektor h,

 

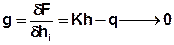
der nun innerhalb des iterativen Prozesses gegen den Wert Null (bzw. hier entsprechend der Eingabe für das Residuum zu 1.0e-08) geführt wird.

 

Der Iterationsprozess, der den Residuenvektor g gegen Null gehen lässt, beinhaltet eine systematische Korrektur einer Folge von Näherungsvektoren h in der folgenden Form:

h_i+1 = h_i + η_i d_{i ,} (i = 0, 1, 2, …)

 

Darin wird der Versuchsvektor h_i des i-ten Iterationsschritts mittels des Iterationsvektors d_i und einer skalaren Schrittweite η_i zum neuen Näherungsvektor h_i+1 verbessert. Der Vektor d_i gibt dabei die Richtung der zum Minimum der Funktion weisenden Relaxation wieder.

Der Iterationsprozess wird abgebrochen, sobald eine zuvor gesetzte Konvergenzschranke/Iterationsdifferenz ε erreicht oder überschritten wird, so dass die zu erzielende Genauigkeit des Ergebnisses durch die Wahl dieses Konvergenzmaßes/Iterationsdifferenz ε bestimmt wird.

Die verschiedenen, an der Ermittlung der Abbruchschranke beteiligten Vektoren werden dabei nachfolgend stets durch Bildung ihrer euklidischen Norm in Beziehung zueinander gesetzt. Dadurch ergibt sich das folgende Abbruchkriterium:

 

 

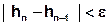
Abflussberechnung

Die Eingaben zur Abflussberechnung werden im Kapitel „Eingaben bei Gewässersystem-Berechnungen“ ausführlich beschrieben.

 

Anfangsbedingungen

Bei Wahl des Moduls SITRA können zusätzlich die Anfangsbedingungen für die stationäre Strömung festgelegt werden. Es besteht die Möglichkeit, die Startpotentiale aus den Eichpotentialen oder aus der Null-Datei zu übernehmen, oder die Startpotentiale können = 0 gesetzt werden.

 

 

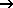Eingaben bei Gewässersystem-Berechnungen