Hydromechanical dispersion describes the distribution or mixing of the same substances (or heat) in moving pore water. This process is caused by the different flow velocities in the pore, the pore size distribution and the path length that the individual material particles can cover.

 

Consideration of dispersive mass transport

 

In addition to advective dispersion, hydromechanical dispersion provides a further flow-dependent component to the mass or energy flow. The mass and energy flow is described in accordance with diffusion using Fick's 1st law:

 

 

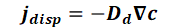
where D_d is the symmetrical dispersion tensor [m²/s]:

 

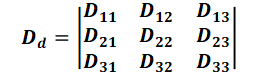
Its coefficients in the three-dimensional view are defined as follows according to Frind (from: FRIND, E.O.; BURNETT, R. D. (1987): Simulation of contaminant transport in three dimensions, 2. dimensionality effects. Water Resour. Res., 23(4), pp. 695-705):

 

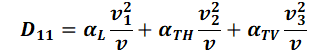
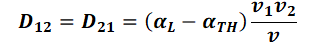
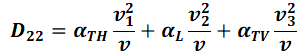
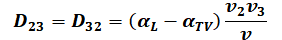
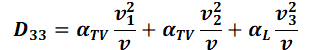
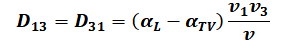
with:

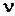= (v₁, v₂, v₃) = velocities in the carthesian coordinate system [m/s],

v = Amount of the field velocity v [m/s],

α_L= longitudinal dispersivity [m],

α_TH = transversal-horizontal dispersivity [m],

α_TV = transversal-vertical dispersivity [m].

 

In two dimensions, the coefficients of the dispersion tensor D_d are defined according to Scheidegger:

 

 

 

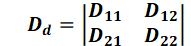
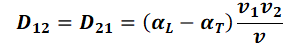
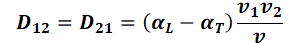
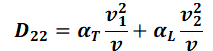
with:

α_T = transversal dispersivity [m],

 

Dispersivity is a characteristic length that can be measured in the laboratory or in the field. It is a geometric measure of the hydraulic conductivity and storage heterogeneity of the aquifer. The order of magnitude of the dispersion coefficient α depends on the scale as well as on porosity, grain shape and grain size.

 

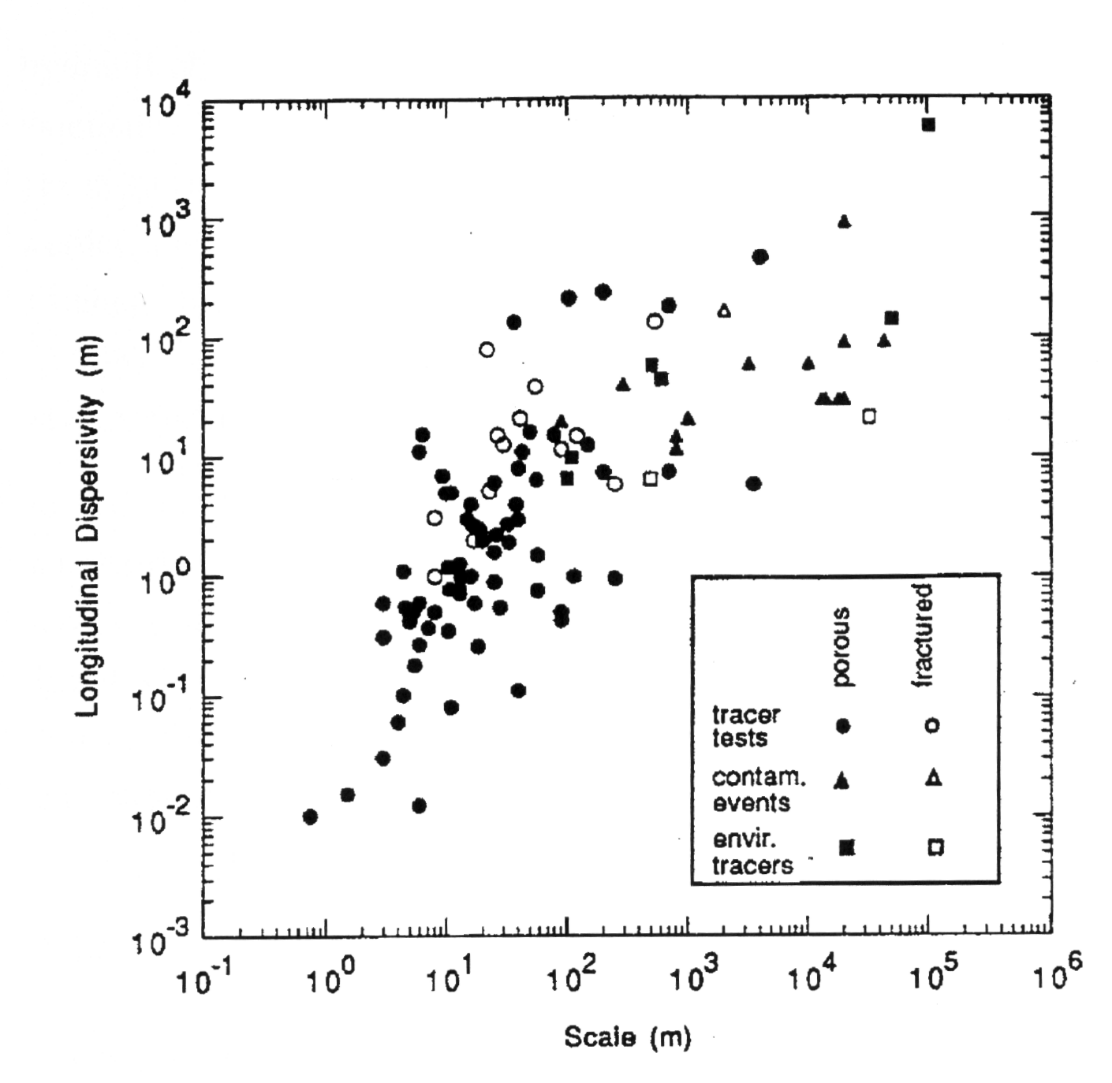
The hydrodynamic (total) dispersion results from the addition of the hydromechanical dispersion and the diffusion.

 

Adsorption