Der nichtlineare Zusammenhang zwischen Kapillardruck und Sättigung wird im Wesentlichen durch die Beschaffenheit des Bodens (Kornform und Korngrößenverteilung) bestimmt. Die folgende Abbildung zeigt schematisch die Druck-Sättigungsbeziehung im Boden:

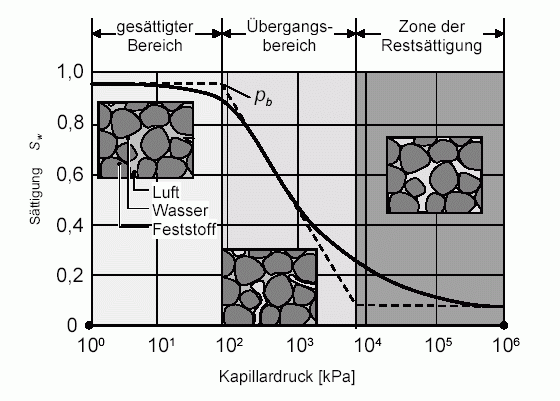
Kapillardruck-Sättigungsbeziehung (p_b entspricht dem Wassereintrittsdruck)

Van Genuchten stellte folgende Beziehung zwischen dem Anteil der ungesättigten an der gesättigten hydraulischen Leitfähigkeit auf:

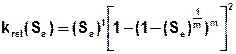
Hierin bedeuten:

S_e = effektive Sättigung

l = unbekannter Parameter für den van Genuchten den Wert 0,5 ermittelt hat

m = 1-1/n = Konstante, n = Porengrößenindex (> 1)

Nach van Genuchten [VAN GENUCHTEN, M. TH. (1980) A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils, Soil Science Society of America Journal. 44: Pages 892-898. 1980] werden für n Werte von 1,5 (tonig) bis 4,5 (sandig) verwendet.

Die effektive Sättigung S_e definiert sich über folgende Formel:

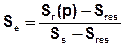
Die Parameter bedeuten:

S_r = relative Sättigung S_r(p)

S_res = Restsättigung = Sättigungsgrad, der je nach Bodentyp infolge von Fließvorgängen nicht unterschritten wird

S_s = maximale Sättigung = Sättigungsgrad, der je nach Bodentyp maximal erreichbar ist (S_s ~1.0)

Die effektive Sättigung steht mit dem Kapillardruck p_c und dem Wassereintrittsdruck p_e in folgender Beziehung:

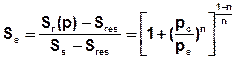
Löst man diese Gleichung nach der druckabhängigen relativen Sättigung S_r(p) auf, erhält man die in SPRING zugrunde gelegte Druck-Sättigungsfunktion nach van Genuchten:

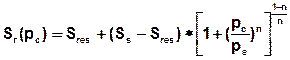
Mit:

p_c = Kapillardruck [N/m²] = [kg/(s²m)]

p_e = Wassereintrittsdruck [N/m²] = [kg/(s²m)]

Der Wassereintrittsdruck ist ein bodenspezifischer Parameter. Er wird als Kehrwert a = 1/p_e in den Sättigungsparametern definiert. Die folgende Abbildung zeigt Beispiele für die Druck-Sättigungsfunktionen nach van Genuchten in Abhängigkeit verschiedener Böden:

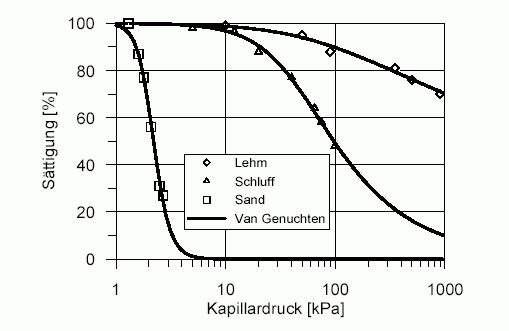
Druck-Sättigungs-Funktion nach van Genuchten

Berechnung der freien Oberfläche (2D)