Das Gesetz von Hubbert liefert die Beziehung zwischen hydrostatischem Druck p und Potential h:

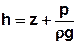
mit:

h = Potential [m]

z = Lagehöhe [m]

p = Druck [N/m²] = [kg/(s²m)]

ρ = Dichte [kg/m³]

g = Erdbeschleunigung [m/s²]

Ein vom durchströmenden Medium unabhängiger Kennwert für die Durchlässigkeit K ist die Permeabilität K_perm. Der Zusammenhang zwischen der Permeabilität K_perm eines porösen Mediums und der Durchlässigkeit K dieses porösen Mediums in Bezug auf ein strömendes Fluid lautet:

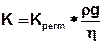
Mit:

K = symmetrischer Tensor für den K_f-Wert [m/s]

K_perm = Permeabilität [m²]

ρ = Dichte [kg/m³]

g = Erdbeschleunigung [m/s²]

η = dynamische Viskosität [kg/(ms)]

Setzt man diese beiden Gleichungen in die vom Potential abhängige stationäre Strömungsgleichung ein, erhält man die stationäre Strömungsgleichung in Abhängigkeit des Drucks:

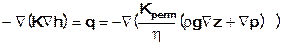
Die Einheit der Gleichung entspricht der des Quellterms q = [1/s].

Da auch ungesättigte Verhältnisse berücksichtigt werden sollen, muss der K_f-Wert K mit einem relativen k-Wert kr_el (0<k_rel<1) skaliert werden.

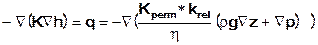
Der Faktor k_rel [-] wird als eine Funktion der Sättigung definiert: k_rel = k_rel (S_r). Im gesättigten Bereich ist k_rel = 1.0.

Die relative Sättigung ist eine vom Druck abhängige Variable S_r = S_r(p), die üblicherweise über eine Funktion nach van Genuchten definiert wird.

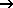Druck-Sättigungsfunktion nach van Genuchten