Die Geometrie des Netzes hat einen unerwünschten Einfluss auf die berechnete Stoffausbreitung, wenn die Elemente zu groß sind bzw. ihre Längserstreckung quer zur Strömungsrichtung liegt. Die folgende Abbildung zeigt, wie sich in Bereichen mit ungünstiger Diskretisierung die Stofffahne wesentlich stärker ausbreitet als bei feinerer Diskretisierung. Dieser Effekt wird als numerische Dispersion bezeichnet.

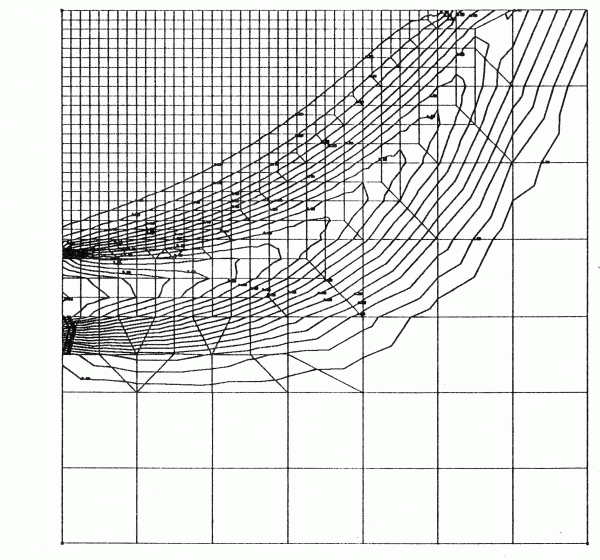
Einfluss der Diskretisierung auf die Ergebnisse der Stofftransportberechnung

(aus: König, C.: Numerische Berechnung des dreidimensionalen Stofftransports im Grundwasser. – Technisch-wissenschaftliche Mitteilungen des Instituts für konstruktiven Ingenieurbau, Ruhr-Universität Bochum, 91-93, (Bochum))

Dieser Effekt kann unter Berücksichtigung der folgenden Kriterien so klein gehalten werden, dass er die natürliche Dispersion nicht übersteigt:

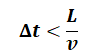
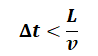und

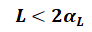
L ist dabei die längste Ausdehnung eines Elements in Strömungsrichtung, α_L ist der Dispersionskoeffizient in longitudinaler Strömungsrichtung.

Oszillationen der numerischen Lösung hängen damit zusammen, dass die Transportgleichung eine Differentialgleichung mit teilweise hyperbolischem Charakter ist, was Schwierigkeiten bereitet, da die verwendeten Algorithmen primär für die Lösung von Differentialgleichungen parabolischen Typs konzipiert sind.

Ist nun der advektive Anteil am Transport groß gegenüber dem dispersiven, so überwiegt der hyperbolische Charakter der Gleichung.

Ein Maß für dieses Verhältnis gibt die Peclet-Zahl P_e, die möglichst kleiner als 2 sein sollte, damit der hyperbolische Anteil nicht zu stark überwiegt.

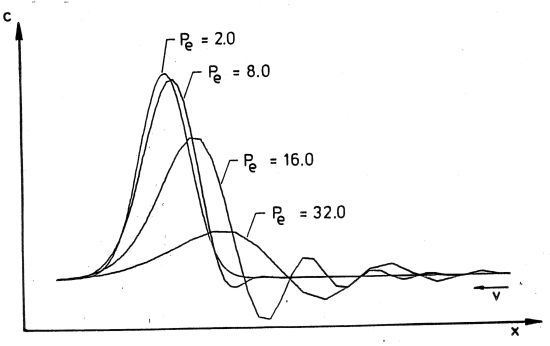
Einfluss der Peclet-Zahl

Sie beschreibt das Verhältnis des Advektionsanteils zum Dispersionsanteil (D) in Bezug zu einer charakteristischen Länge (Kantenlänge der Elemente, Δl)

Je niedriger die Peclet-Zahlen werden, desto weniger Iterationen sind notwendig, um einen zuvor definierten Maximalwert der Residuen zu erreichen. Sobald diese dimensionslose Kennzahl den Wert 10 überschreitet, ist nicht mehr gewährleistet, dass die Lösung konvergiert. Eine optimale Ortsdiskretisierung ergibt sich bei einer Peclet-Zahl < 2.

Zeitdiskretisierung