Bei der Änderung des relativen K-Werts in einem Element erfolgt durch Berücksichtigung der K-Werte der benachbarten Elemente automatisch eine lokale Dämpfung.

Mit dieser Dämpfung werden die durch die Iteration entstehenden starken Schwankungen der K-Werte angrenzender Elemente verringert. Für jedes Element wird die berechnete relative Änderung (in %) des K-Wertes noch einmal in Beziehung zu den relativen Änderungen der K-Werte in den Nachbarelementen geglättet. Die Vorgehensweise lässt sich am einfachsten an einem Beispiel (2D) erläutern:

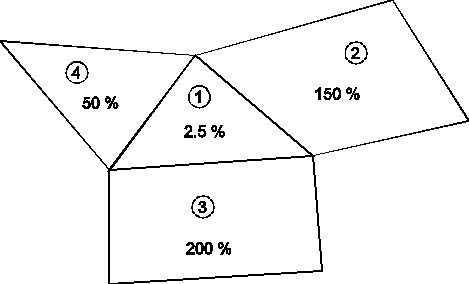
Die Änderung des K-Wertes in Element 1 berechnet sich nun als Mittelwert aus:

• berechneter % - Änderung in Element 1 und

• mittlerer % - Änderung in den Nachbarelementen

wie folgt:

½ * (2,5 % + (150 % + 200 % + 50 %)/3) = ½ * (2,5 % + 133,33 %) = 67,92 %

Der K-Wert in Element 1 wird auf 67,92 % von 0,40 = 0,271 gesetzt.

Bei 3D-Modellen gehen zusätzlich zu den horizontal angrenzenden Nachbarelementen auch die vertikal angrenzenden Elemente in die Berechnung ein. Eine Berücksichtigung von „Schichtungen“, d.h., Bereiche mit K-Werten unterschiedlicher Größenordnungen (Leiter/Stauer) ist ebenfalls automatisch vorgesehen: Nachbarelemente mit K-Werten anderer Größenordnungen gehen in die Wichtung mit kleineren Wichtungsfaktoren ein.

Eingabeparameter