This time the unsaturated parts of the aquifer are fully included in the finite element calculation. The algorithm uses the pressure equation. At each node, the saturation Sr = Sr(p) is obtained from the actual pressure p. Based on the saturation at all nodes, the relative K-value kr = kr(Sr) for each element is computed:
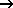Saturation Sr, i+1 and relative K-value kr, i+1with: i = iteration step
The change of the relative permeability from one step to the other is attenuated with the attenuation factor 0 < w < 1 to avoid oscillations:
with: i = iteration step
For w=1.0, the iteration is not attenuated at all; for w=0, the attenuation is maximum. The default value is 0.5. The initial state for the iteration is either obtained by relative permeabilities computed from initial potential heads (EICH), from the potential heads stored in the null-file or from the attribute ASAT (initial saturation). Else, the relative permeabilities must have the initial value 1.0.
The iteration process continues until the difference between the two computed potential heads is less than the user-defined limit (limit of iterations).
Remark:
Poorly-chosen parameters can lead to numerical problems in the iteration of the free surface. In the worst case, the iteration may not converge to a solution.
The main reason for this is high areal recharge rates in unsaturated areas. These can cause oscillations.
In the case that the elements are "open" (k = 1 or rather kr = 1), the free surface drops beneath the elevation of the elements. Hence it follows that the elements are unsaturated in the next iteration step, thus made "impermeable" (k 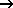0 or rather. kr - 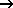0). Then, high areal recharge rates cause a "potential head mound" above these impermeable elements. Therefore, in the next step they will have full saturation again.
A strong attenuation coefficient can, in most cases, prevent the oscillations. However, the attenuated iteration takes longer to converge, so the number of iteration steps must be increased.