The geometry of the mesh has an undesirable effect on the computed material spreading, if the elements are too large and their length is perpendicular to the flow direction. The following figure shows how in areas with unfavourable discretization the material spreads much more than in areas with finer discretization. This effect is known as numerical dispersion.

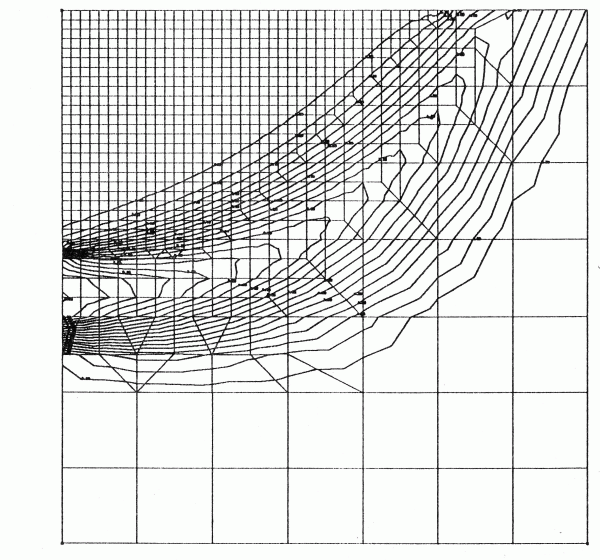
Influence of the discretization on the results of the mass transport calcultion

(from: König, C.: Numerical computation of the three-dimensional mass flow in the groundwater. – Technisch-wissenschaftliche Mitteilungen des Instituts für konstruktiven Ingenieurbau, Ruhr-Universität Bochum, 91-93, (Bochum))

Taking into account the following criteria this effect can be so small that it does not exceed the natural dispersion:

and

L is the longest dimension of an element in the flow direction, is the dispersion coefficient in longitudinal flow direction.

Oscillations of the numerical solution are related to the fact that the transport equation is a differential equation with partially hyperbolic character. This is difficult because the algorithms used are designed primarily for the solution of differential equations of parabolic type. Now if the part of the advective transport is large compared to the dispersive part, the hyperbolical character of the equation outweighs.

A measure of this ratio is the Peclet number P_e, which should be less than 2 so that the proportion of the non-hyperbolic part predominates.

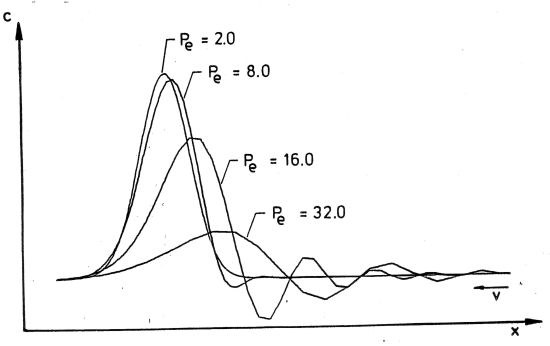
Influence of the Peclet number

 

 

It describes the ratio of the advective part to the dispersion part (D) with respect to a characteristic length (side length of the elements,).

The lower the Peclet number, the less iterations are necessary to achieve a predefined maximum value of the residuals. Once this dimensionless number exceeds the value 10, is no longer guaranteed that the solution converges. An optimal discretization in space results for a Peclet number < 2.

 

Time discretization