For a saturated aquifer with constant density and steady state flow the mass flux j for the mass transport can be mathematically formulated as follows:
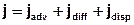
Since the transport of the ingredient takes only place in the effective pore volume (n) of the aquifer, it must be additionally introduced for a volume based consideration.
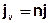
By substituting the components we obtain the equation:
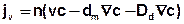
The proportion of the molecular diffusion and hydromechanical dispersion can be summarized to the hydrodynamic dispersion:
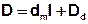
With the standard matrix I:
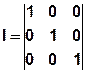
Results the equation for the steady state mass flow:
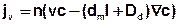
The mass balance allows the consideration of the change in concentration over time, referred to in a control volume in- and outflowing mass quantities and taking into account sources and sinks (σ), that means, points at which the system is supplied with substances or at which substances are removed from the system.
The term σ represents all mass in- and outputs, and can be broken down as follows:
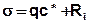
with:
qc* = volume-related addition or removal of water with the concentration c*
Ri = Share of all non-conservative mass transport processes such as sorption, chemical or biological degradation reactions
Using the product rule for the advection term:
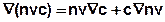
of the continuity condition
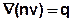
and the summary 
results the transient transport equation for ideal tracer at a constant density of the aquifer to:
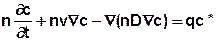
[Example: q corresponds e.g. to the attribute node removal/addition KNOT or to a reaction rate, unit [m³/TU] and c* corresponds to the attribute KONZ]
If saturated/unsaturated conditions exist in the aquifer the saturation Sr must be taken into account in the transport equation:
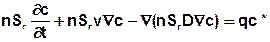
The unit of this equation results in [kg mass / (kg solution *s)] or [kg mass / (m³ solution *s)], dependent on the unit of the concentration boundary condition.
Treatment on non-conservative processes