The following figure gives an overview of the non-conservative mass transfer processes:

 

Nicht-konservative Stofftransportprozesse

 

When including the adsorption processes in the transport equation is to be noted that the total mass of the considered ingredient in a reference volume not only consists of the dissolved and transported amount of material (nc), but also of the amount of adsorbed substances 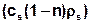. The concentration of the adsorbed substance (c_s) is referred to the solids fraction (1-n), where the density of the matrix (ρ_s) must additionally be taken into account.

In this case, the term

 

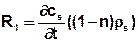
Has to be taken into the transport equation with:

c_s = adsorbed concentration in the matrix [kg/kg]

ρ_s = Density of the matrix [kg/m³]

 

The adsorption rate is described by a function c_s = f (c), either after the adsorption isotherm based on

Henry, Freundlich or Langmuir.

 

By the integration of production and decay is important to note that this theoretically occurs both in the fluid and in the matrix. The corresponding term R therefore consists of two parts with different decay and production functions for the solution in the fluid f(c) and the adsorbed materials in the matrix f_s(c_s):

 

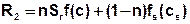
During the mass transfer calculation in SPRING production and decay processes will be considered only in the fluid, because separation of these processes is impossible in nature.

Due to the irreversibility of these processes here, there is no storing!

Instead of production and decay it is possible to realize a half-life calculation. The corresponding term is then:

 

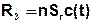
with:

 

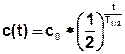
Boundary and initial conditions