For a saturated aquifer with constant density and steady state flow, the total mass flow j for mass transport can be mathematically formulated as the sum of the individual mass flows from advection (j_adv), diffusion (j_diff) and dispersion (j_disp) as follows:

j = j_adv + j_diff + j_disp

As the transport of the constituent only takes place in the flow-effective pore space (n) of the aquifer, this must also be introduced in a volume-based analysis.

j_v = nj

 

with:

j_v = volume-related total mass flow [(m kg)/(s kg)]

n = flow-effective pore space [-]

j = total mass flow [(m kg)/(s kg)]

 

The equation is obtained by substituting the individual components:

 

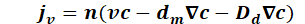
The proportion of molecular diffusion and hydromechanical dispersion can be summarised as hydrodynamic dispersion:

 

D = d_mI + D_d

 

With the unit matrix I:

 

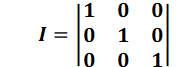
This results in the equation for the steady state mass flow:

 

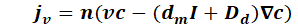
The mass balance makes it possible to observe the change in concentration over time (transient mass transport) in relation to the rates of substance flowing into or out of a control volume, taking into account sources and sinks (σ), i.e. points at which substance is added to or removed from the system.

 

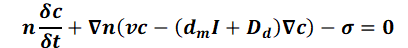
The term σ represents all mass in- and outputs, and can be broken down as follows:

 

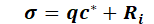
with:

qc* = volume-related addition or removal of water with the concentration c*

R_i = proportions of all non-conservative mass transport processes such as adsorption, chemical or biological degradation reactions

 

Using the product rule for the advection term:

 

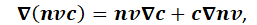
the continuity condition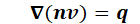

and the summary D = d_mI + D_d

gives the transient mass transport equation for ideal tracers at constant density of the aquifer:

 

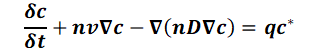
Example:

q corresponds, for example, to the attribute KNOT node removal/addition or a mass flow rate, unit [m³/TU] and c* corresponds to the corresponding attribute KONZ.

If saturated/unsaturated conditions are present in the aquifer, the saturation S_r must be taken into account in the mass transport equation:

 

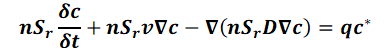
Depending on the unit of the concentration boundary condition, the unit of this equation is [kg substance / (kg solution *s)] or [kg substance / (m³ solution *s)].

 

Treatment on non-conservative processes