Hubbert's law provides the relationship between hydrostatic pressure p and potential h:

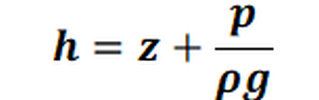
with:

h = potential head [m]

z = position height [m]

p = pressure [N/m²] = [kg/(s²m)]

ρ = density [kg/m³]

g = gravitational acceleration [m/s²]

A characteristic value for the hydraulic conductivity K that is independent of the flowing medium is the permeability Kperm. The relationship between the permeability Kperm of a porous medium and the hydraulic conductivity K of this porous medium in relation to a flowing fluid is as follows:

with:

K = symmetrical tensor for the K-value [m/s]

K_perm = Permeability [m²]

ρ = Density [kg/m³]

g = gravitational acceleration [m/s²]

η = dynamic viscosity [kg/(ms)]

If these two equations are inserted into the steady state flow equation dependent on the potential head, the steady state flow equation is obtained as a function of the pressure:

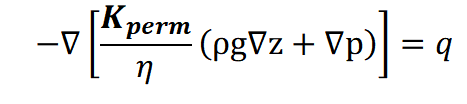
The unit of the equation corresponds to that of the source term q = [1/s].

As unsaturated ratios should also be taken into account, the K_f value K must be scaled with a relative k value krel (0<krel<1).

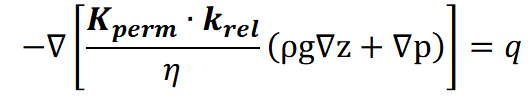
The factor krel [-] is defined as a function of saturation: krel = krel (Sr). In the saturated range, krel = 1.0.

The relative saturation is a pressure-dependent variable Sr = Sr(p), which is usually defined using a van Genuchten function.

Pressure-saturation function according to van Genuchten