The non-linear relationship between capillary pressure and saturation is essentially determined by the nature of the soil (grain shape and grain size distribution). The following figure schematically shows the pressure-saturation relationship in the soil:

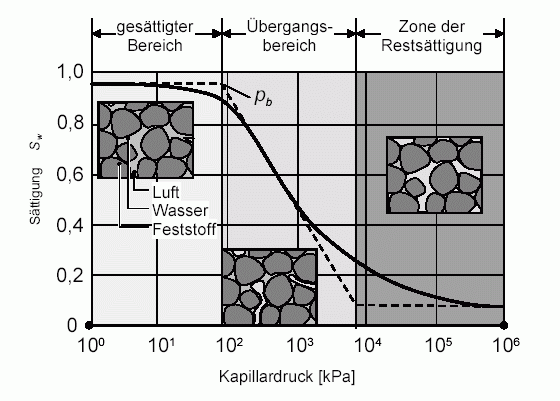
Capillary pressure-saturation relationship (pb corresponds to the water inlet pressure)

Van Genuchten established the following relationship between the proportion of unsaturated and saturated hydraulic conductivity:

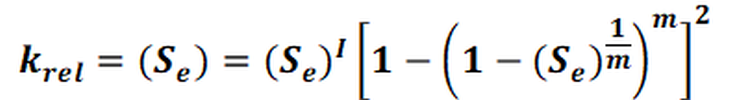
This means:

S_e = effective saturation

l = unknown parameter for which van Genuchten has determined the value 0.50,

m = 1-1/n = constant, n = pore size index (> 1)

According to van Genuchten [VAN GENUCHTEN, M. TH. (1980) A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils, Soil Science Society of America Journal. 44: Pages 892-898. 1980] n values from 1.5 (clayey) to 4.5 (sandy) are used.

The effective saturation is defined by the following formula:

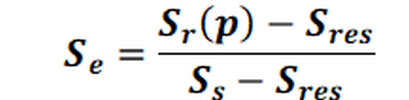
The parameters mean:

S_r = relative saturation S_r(p)

S_res = Residual saturation = degree of saturation which, depending on the soil type, the soil does not fall below as a result of flow processes

S_s = maximum saturation = maximum degree of saturation that can be achieved depending on the soil type (Ss ~1.0)

The effective saturation is related to the capillary pressure pc and the water inlet pressure pe as follows:

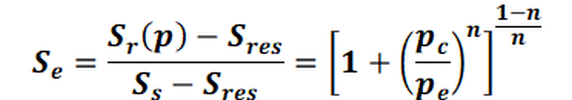
If this equation is solved according to the pressure-dependent relative saturation Sr(p), the pressure saturation function according to van Genuchten used in SPRING is obtained.

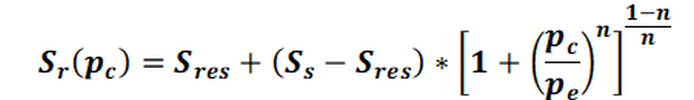
With:

p_c = capillary pressure [N/m²] = [kg/(s²m)]

p_e = water inlet pressure [N/m²] = [kg/(s²m)]

The water inlet pressure is a soil-specific parameter. It is defined as the reciprocal value a = 1/p_e in the saturation parameters. The following figure shows examples of the pressure-saturation functions according to van Genuchten as a function of different soils:

Pressure-saturation functions according to van Genuchten

Calculation of the free surface (2D)