Das Gesetz der Energieerhaltung lässt sich mit Hilfe der beiden Größen

 

c_w = spezifische Wärmekapazität des Fluids [J/(kg K)]

c_s = spezifische Wärmekapazität der Matrix [J/(kg K)]

 

unter Berücksichtigung des Porenraums n wie folgt mathematisch formulieren:

 

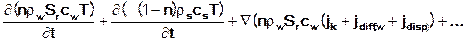
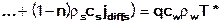
Hierbei stellt die rechte Seite der Gleichung die Summe aller Energiequellen- und –senken und T* die Temperatur zu- und abfließender Mengen dar.

In diese Gleichung werden die Wärmeflüsse für Konvektion, Dispersion und Wärmeleitung eingesetzt. Unter Anwendung der Produktregel für den Konvektionsterm und der Kontinuitätsbedingung

(vgl. Stofftransport ):

 

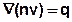
ergibt sich die instationäre Energietransportgleichung zu:

 

 

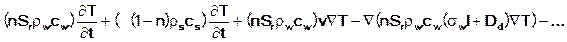
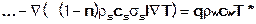
Dabei werden die Wärmediffusionsparameter 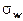[m²/s] und 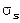[m²/s] durch

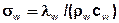
und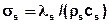

 

definiert.

 

mit:

ρ_w,s = Dichte des Fluids (w) oder der Matrix (s) [kg/m³]

c_w,s = spezifische Wärmekapazität [Ws /(kg K)]

λ_w,s = Wärmeleitfähigkeit [W / (m K)]

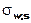= Diffusionsparameter = λ_w,s / (ρ_w,s c_w,s) = [m²/s]

I = Einheitsmatrix [-]

D = Dispersionstensor [m²/s]

Sr = Sättigungsgrad [-]

n = durchflusswirksamer Porenraum [-]

v = Abstandsgeschwindigkeit [m/s]

q = div v (aus Kontinuitätsbedingung) [1/s]

T = Temperatur [K]

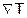= Temperaturgradient [K/m]

T* = veränderlicher Temperaturzu-/abfluss [K]

 

Die Energietransportgleichung hat ebenso wie die Wärmeproduktionsrate (QKON) die Einheit [W/m³] = [J/(m³s)].

 

Rand- und Anfangsbedingungen