Als Ortsdiskretisierung wird die Zerlegung des Untersuchungsgebiets in einzelne, geometrisch einfach Teilgebiete (hier: Dreiecke, Vierecke, Prismen), die finiten Elemente bezeichnet. Innerhalb eines Elementes wird die Untersuchungsgröße (hier: Potential, Temperatur, Konzentration) durch Ansatzfunktionen angenähert. Stützstellen für die Annäherung des Funktionsverlaufs sind die Knoten. Die Knoten liegen in den Elementecken und ggf. auf den Elementkanten und verbinden alle angrenzenden Elemente miteinander, wodurch ein zusammenhängendes Gebiet entsteht.

Das komplexe Differentialgleichungssystem, durch das die physikalischen Prozesse (hier: Strömungs- und Transportprozesse in porösen Medien) beschrieben werden, wird durch diese Approximation des Untersuchungsgrößenverlaufs auf Elementebene auf ein diskretes Gleichungssystem für die Lösung der Untersuchungsgrößen in den Knoten reduziert. Der Wert der Untersuchungsgröße innerhalb eines Elementes kann anschließend aus den berechneten Knotenwerten interpoliert werden.

Über die Knoten sind die Elemente des Gebiets untereinander verbunden, damit ist der angenäherte Verlauf der Untersuchungsgröße auch über die Elementkanten hinweg stetig. In wieweit auch die Ableitungen der Untersuchungsgrößen stetig sein müssen, hängt von dem physikalischen Problem ab. Für Strömungs- und Transportberechnungen in porösen Medien ist die Stetigkeit in der Untersuchungsgröße ausreichend, weswegen Finite Elemente mit linearen Ansatzfunktionen ausreichend genau sind. Bei Verwendung linearer Ansatzfunktionen liegen die Knoten in den Elementecken.

Die Ansatzfunktionen, auch Formfunktionen genannt, sind Funktionen, die bei der Methode der finiten Elemente den realen Funktionsverlauf über dem Element bestmöglich annähern. Bedingung dabei ist die Erfüllung der Stetigkeitsbedingung. Da die Knotenpunkte von jeweils mindestens zwei Elementen geteilt werden, wird bei Verwendung der Werte in diesen Punkten die Stetigkeitsbedingung erfüllt. Der gesuchte Funktionsverlauf wird durch Interpolation der Werte in diesen Knotenpunkten näherungsweise bestimmt. Um den Funktionsverlauf u(x, y) durch die Knotenpunkte auszudrücken, verwendet man die Formfunktionen. Diese besitzen die Eigenschaft, im aktuellen Knoten stets 1 und in den restlichen Knoten 0 zu sein, so dass sich u(x, y) als Summe über die Anzahl der Knoten von u_i * N_i(x, y) ergibt, wobei i die Nummer des Knotens im Element und u den Wert am Knoten darstellt (abgeleitet aus Wikipedia).

Die lineare Formfunktion für das Einheitsdreieck mit den Koordinaten der drei Eckpunkte (0,0), (1,0), (0,1) sieht wie folgt aus (linearer Ansatz):

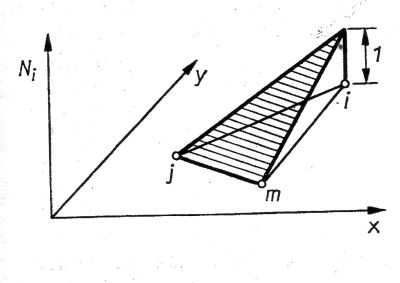
Lineare Ansatzfunktion für ein Dreieck

Für Viereckelemente muss ein bilinearer Ansatz verwendet werden, da die Kante eines Viereckelements mit einer Z-Koordinate ungleich 0 keine Gerade, sondern eine gebogene Linie darstellt (folgende Abbildung):

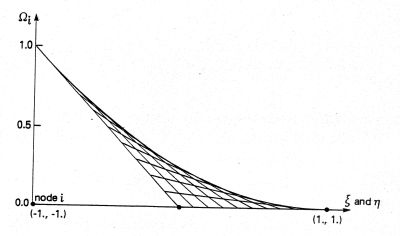
Bilineare Ansatzfunktion für ein Viereck

Noch deutlicher wird die Ansatzfunktion in folgender Abbildung:

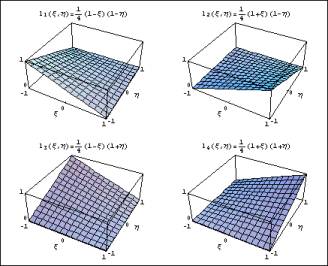
Bilineare Ansatzfunktion im Viereckelement

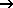Umsetzung in SPRING