Der wichtigste Schritt für eine Interpolation mit dem Krigingverfahren ist daher die Erstellung eines Variogramms. Dieses dient dazu, die Differenz je zweier Messwerte zum Abstand der zugehörigen Messpunkte in Beziehung zu setzen und die so gewonnene statistische Information durch eine Varianz-Funktion sinnvoll zu approximieren:

 

Es wird in einem ersten Schritt ein so genanntes experimentelles Variogramm erstellt. Dazu werden Abstandsklassen (Abstände in Metern) definiert:

mit

 

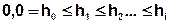
Für jede Abstandsklasse werden die Messwerte aller Messpunktpaare, deren Abstände in diese Klasse fallen, ausgewertet und eine Semivarianz g_k(h) berechnet:

mit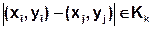

 

 

wobei m_k die Anzahl aller Messpunktpaare (i, j) bezeichnet, deren Abstand in der Klasse K_k liegt.

z_j bezeichnet einen Punkt, der um den Abstand h von z_i entfernt ist.

 

Für die vom Benutzer gewählte Unterteilung der Abstandsklassen (maximal 16) wird eine Tabelle mit den wichtigsten Variogrammdaten aller Abstandsklassen ausgegeben:

 

Spalte 1: Nummer der Klasse k,

Spalte 2: maximaler Abstand h_k,

Spalte 3: mittlerer Abstand h aller Messpunktpaare in dieser Klasse,

Spalte 4: Semivarianz g_k(h)

Spalte 5: Anzahl aller Messpunktpaare in dieser Klasse m_k,

Spalte 6 und 7: imax und jmax, Nummern der Messpunkte, für die die Messwerte z(imax) und z(jmax) den größten Werteunterschied der Abstandsklasse aufweisen,

Spalte 8: d(z(imax),z(jmax)) = 0.5 * (z(imax)-z(jmax))², als Vergleichswert für die Varianz g_k(h)

 

Eine solche Tabelle kann z.B. für 10 Abstandsklassen bei einer äquidistanten Unterteilung der Klassen folgendermaßen aussehen:

 

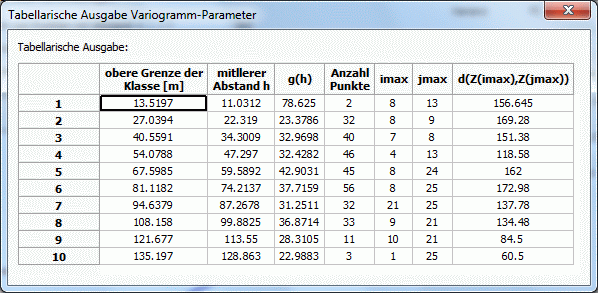
Tabellarische Ausgabe der Variogrammparameter

 

Außerdem wird zur Orientierung der maximale Abstand zwischen zwei Messwerten protokolliert.

Die Abstandsklassen sollten möglichst so eingeteilt werden, dass in keiner Klasse die Anzahl der zugehörigen Messpunktepaare = 0 wird. Die Anzahl sollte für alle Abstandsklassen in der gleichen Größenordnung liegen. Liegt ein Messpunktepaar in keiner Abstandsklasse, so wird der maximale Abstand der letzten Klasse entsprechend vergrößert.

In einem experimentellen Variogramm werden nun die berechneten Varianzen g_k(h) (Spalte 4 der Tabelle = y-Achse) zu den mittleren Abständen h (Spalte 3 der Tabelle = x-Achse) in einem Diagramm aufgetragen. Begrenzung der x-Achse ist der ermittelte maximale Abstand der Messpunkte zueinander.

Es muss nun eine Funktion gefunden werden, die dieses experimentelle Variogramm möglichst gut approximiert und zur Berechnung der Interpolationsgewichte λ_i(x, y) verwendet werden kann.

Als Ansatzfunktionen hierfür werden 6 Funktionstypen angeboten:

• Variogramm h^A

• Sphärisches Variogramm

• Exponentielles Variogramm

• Gauß-Variogramm

• Kubisches Polynom

• Ausgleichspolynom

 

Für die Typen (1) bis (5) müssen die Parameter PEP, PI und A festgelegt werden:

• PEP >= 0: sogenannter 'nugget effect': Maß für die Streuung des Messwertes (Messfehler) g(0)=PEP

• PI >= 0: Varianz der beobachteten Messwerte

• A >= 0: Größe des Bereichs, dessen Punkte zur Interpolation verwendet werden, bei den Funktionstypen (2) bis (5) sollte der Parameter A ungefähr dem max. Abstand entsprechen

 

In der folgenden Abbildung ist die Bedeutung der einzelnen Parameter schematisch dargestellt:

 

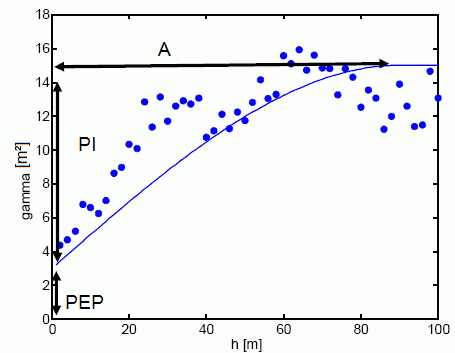
Schematische Darstellung der Variogramm-Parameter

 

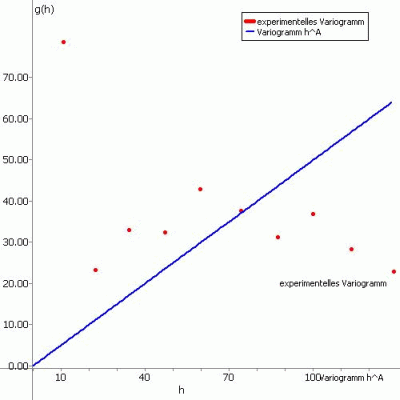
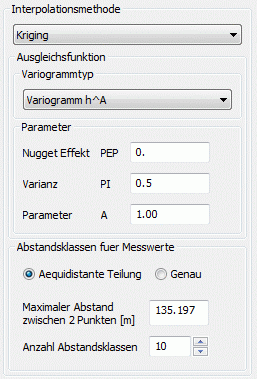
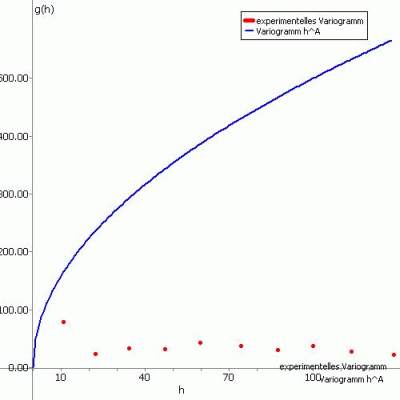
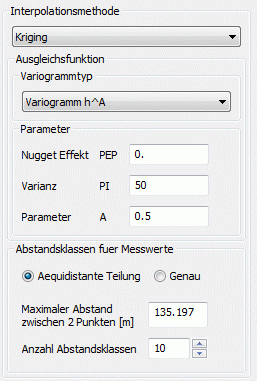
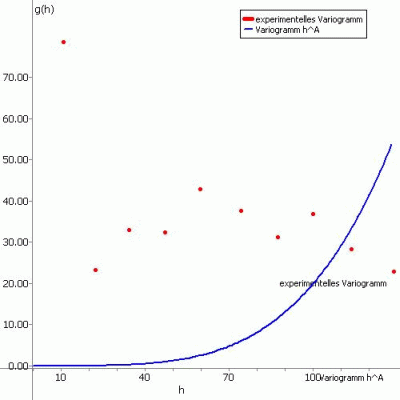
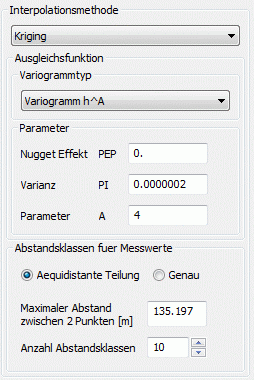
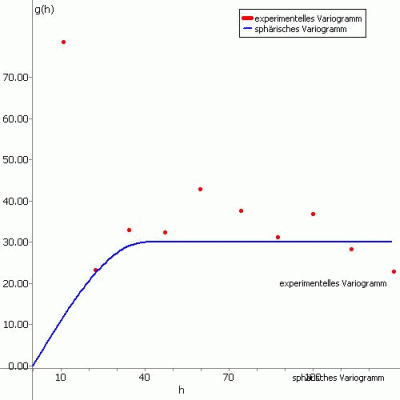
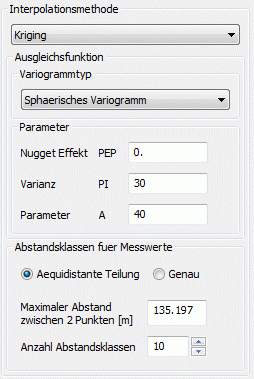
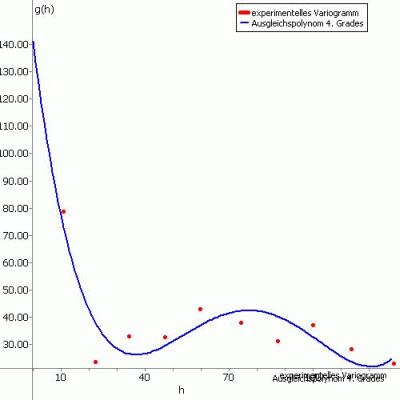
Die folgenden Abbildungen zeigen das experimentelle Variogramm (rote Punkte) überlagert mit der gewählten Funktion (blau) und der zugehörigen Eingabe in SPRING für die verschiedenen Ansatzfunktionen.

 

(1) Variogramm h^A:

Die Ansatzfunktion für diesen Variogrammtyp lautet:

g(h) = PEP + PI * h^A

 

In Abhängigkeit des Parameters A gibt es drei verschiedene Funktionsverläufe des Variogramms:

 

Fall 1: A = 1 (Gerade)

 

 

Fall 2: A < 1

 

 

Fall 3: A > 1

 

 

 

(2) sphärisches Variogramm:

Die Ansatzfunktion für diesen Variogrammtyp lautet:

 

 

 

 

 

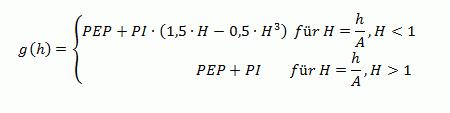
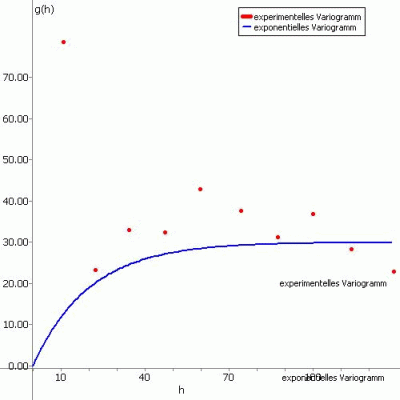
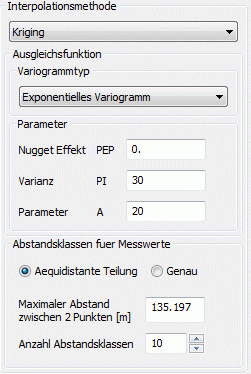
(3) exponentielles Variogramm:

Die Ansatzfunktion für diesen Variogrammtyp lautet:

 

g(h) = PEP + PI * ( 1-exp (-H)), mit H = h/A

 

 

 

 

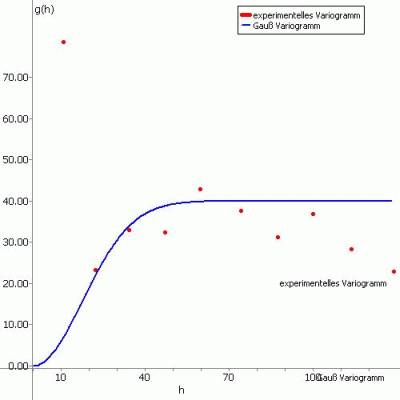
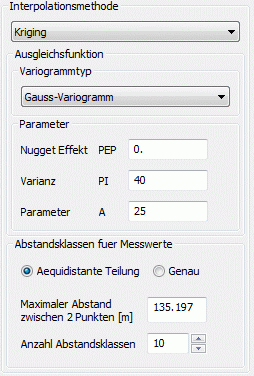
(4) Gauss Variogramm:

Die Ansatzfunktion für diesen Variogrammtyp lautet:

 

g(h) = PEP + PI *( 1-exp (-H²)), mit H = h/A

 

 

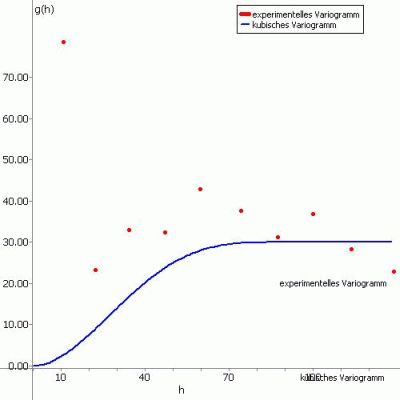
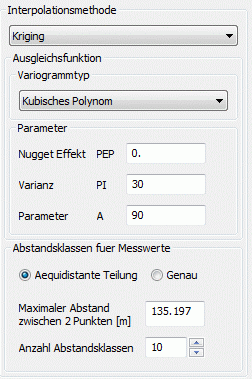
(5) kubisches Variogramm:

Die Ansatzfunktion für diesen Variogrammtyp lautet:

 

 

 

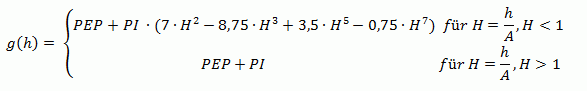
(6) Ausgleichspolynom vom Grad 1 bis 9

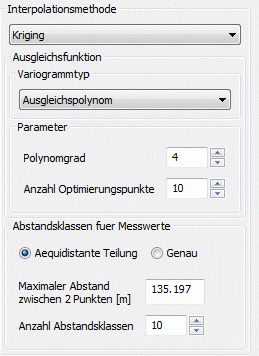
Wird ein Ausgleichspolynom gewählt, müssen der Grad des Polynoms (zwischen 1 und 9) und die Anzahl der Punkte, für die das Polynom approximiert werden soll (maximale Anzahl ist die Anzahl der Abstandsklassen), festgelegt werden.

 

Für das obige Beispiel ergibt sich z. B. folgendes Ausgleichspolynom:

 

 

Grundsätzlich sollten die entsprechend konstruierten Funktionen monoton steigend sein und die berechneten Werte möglichst gut approximieren. Die Güte der Varianz-Funktion g(h) bestimmt letztendlich auch die Güte der mit Kriging interpolierten Punkte.

Auf die Erstellung des Variogramms ist bei Verwendung des Kriging-Interpolationsverfahrens besonderen Wert zu legen, da das Interpolationsverfahren besonders sensibel auf die Wahl der Parameter reagiert.

 

Kriging Interpolation