Ziel der inversen Modellierung ist die Minimierung der Zielfunktion. Die Zielfunktion setzt sich aus zwei Hauptanteilen zusammen:

 

ZF = ZF_obs+ ZF_par

 

Es gehen sowohl die gemessenen Werte (ZF_obs, z.B. Potentiale, Mengen) als auch die Schätzwerte der Parameter (ZF_par, z.B. K-Werte, Leakagekoeffizienten, Speicherkoeffizienten) in die Zielfunktion ein. Die Anteile werden weiter aufgeteilt:

 

ZF_obs = ZF_POTE + ZF_LEAK + ZF_KNOT

ZF_par = ZF_KWER+ZF_LERA + ZF_KSPE

 

Um die Zielfunktion zu ermitteln, wird jedem Parameter und Messwert eine Standardabweichung 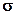zugeordnet. Diese entspricht etwa dem zu erwartenden Fehler der Größe.

Jeder Messwert m und jeder Parameterwert p wird nach jedem Schritt der inversen Kalibrierung wie folgt ausgewertet (Methode vom Typ 'kleinste Quadrate' (least squares)):

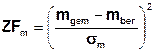bzw.

 

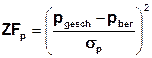
Für die numerische Lösung dieses nichtlinearen Minimierungsproblems werden bei der inversen Modellierung in SPRING zwei verschiedene mathematische Algorithmen angeboten:

• ein Gauß-Newton-Verfahren nach Levenberg-Marquard und

• ein Gradienten-Verfahren nach der Quasi-Newton-Methode

 

Die Zielfunktionsanteile jedes Messwertes und jedes Parameters werden summiert. Bei Wahl einer kleinen Standardabweichung 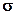, resultiert ein großer Anteil an der Zielfunktion und somit eine hohe Gewichtung. Aus einer großen Standardabweichung 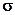resultiert ein kleiner Anteil an der Zielfunktion und somit eine kleine Gewichtung.

Die folgende Tabelle soll den Einfluss der Gewichtung aufzeigen.

1. Zuerst sind die zwei Potentiale H1 und H2 aufgelistet. Das Residuum ist für beide Messstellen gleich, jedoch ergibt sich ein hundertfach größerer Anteil an der Zielfunktion für H2, da dieser Wert mit 10 cm Standardabweichung stärker gewichtet ist als H1 mit 1 m Standardabweichung.

2. Ein anderer Effekt lässt sich mit den Mengen Q1 und Q2 veranschaulichen. Je nachdem, in welcher Einheit gerechnet bzw. ausgewertet wird, ergibt sich bei gleicher Standardabweichung eine andere Gewichtung.

3. Deshalb sollten für Mengen immer Standardabweichungen im Bereich von 10-25% der Messungen (je nach Genauigkeit) gewählt werden. Q1* und Q2* haben eine Standardabweichung von 10% - die Anteile der Zielfunktion sind in der gleichen Größenordnung.

4. Als letzte Beispielgröße ist ein Parameterwert für den K-Wert dargestellt. Da dieser Wert logarithmisch verarbeitet wird, sollte die Standardabweichung in Größenordnungen angegeben werden (0.1,…, 1).

 

 

 

Die folgende Abbildung soll vereinfacht aufzeigen, weshalb die Startwerte der Parameter entscheidend sein können. Die Zielfunktion ist für verschiedene Parameterwerte unterschiedlich groß. Es gibt ein absolutes Minimum, sowie diverse lokale Minima. Startet man die inverse Modellierung zum Beispiel mit dem Startparameter 1, strebt die Zielfunktion in das zugehörige lokale Minimum. Die Zielfunktion für den Startparameter 2 befindet sich auf einem lokalen Maximum und kann in eines der beiden lokalen Minima streben. Die Zielfunktion ist für den Startparameter 3 am höchsten, jedoch kann der Algorithmus von diesem Startpunkt aus das absolute Minimum erreichen. Es ist also durchaus sinnvoll, den Optimierungsprozess mehrmals mit verschiedenen Parameterwerten zu starten.

 

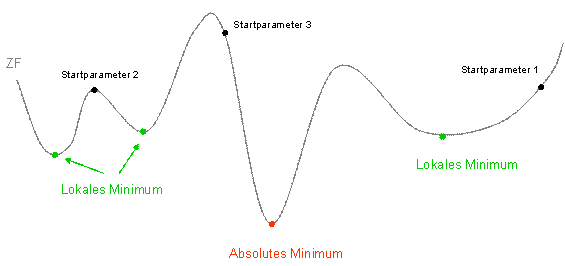
Zielfunktion der inversen Modellierung

 

Umsetzung in SPRING