Viscosity

Viscosity is a property that is due to the inner friction of the fluid. The unit of the viscosity is [kg/m s)] or Pascal-second [Pa s].

The dynamic fluid viscosity η [kg/(m s)] and, with a large temperature gradient, the density ρ [kg/m³] are temperature-dependent variables. Their change due to the temperature has the consequence that the differential equations (the transient flow and the energy transport equation) represent a coupled differential equation system.

An experimental formula for describing the relationship between dynamic fluid viscosity and temperature is used in the calculation:

 

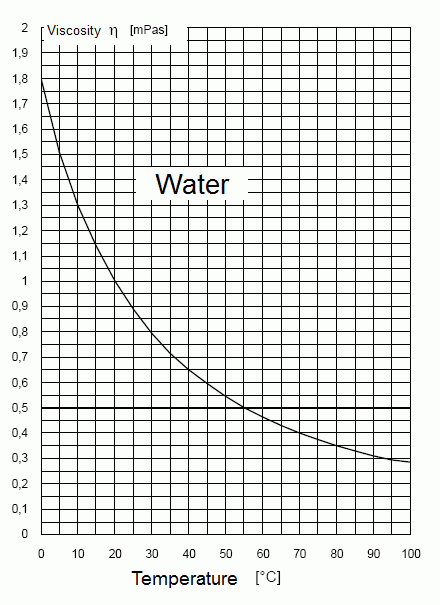
Dynamic viscosity η of water dependent on the temperature at a density of ρ= 1000.0 [kg/m³]

The unit millipascal second [mPa s] corresponds to the unit 1000*[kg/(m s)].

 

The following relationship applies for dynamic and kinematic viscosity:

dynamic viscosity: η = μ * ρ [kg/(m s)]

kinematic viscosity: μ = η / ρ [m²/s]

 

Temperature-dependent density

The linear dependency of the density [kg/m3] from the temperature T [°C] is considered in SPRING:

 

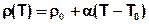
With:

ρ(T) = temperature dependent density [kg/m³]

 

ρ₀ = density of the reference temperature T₀ in [kg/m³], default is ρ₀ = 1000.0 [kg/m³]:

 

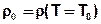
T₀ = Reference temperature [°C], default is T₀ = 20°C

α = constant density gradient, default is α = 0.0

 

The following figure shows the dependency of the density from the temperature:

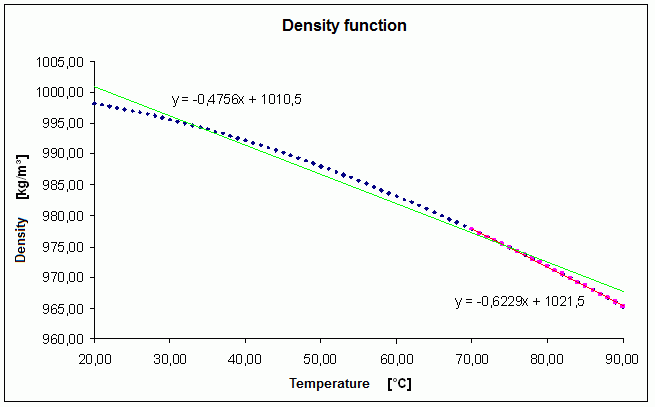
Temperature-dependent density function

 

In this case is:

ρ₀ = ρ(T₀=20 °C) = 1010,5 [kg/m³]

The density function is approximated by a linear equation (green line) in the considered temperature interval (here: about 32 – 75 °C), by this the density gradient α is defined.

 

Here, the density gradient α = constant = -0.4756. (This corresponds to the slope (= 1st derivative) of the line):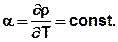

If the initial or computed temperatures lie at a different temperature range, another fit line is to be defined (red line).

 

Realization in SPRING