Using the two variables:
cw = specific heat capacity of the fluids [J/(kg K)]
cs = specific heat capacity of the matrix [J/(kg K)]
and considering the pore volume n the law of conservation of energy can be mathematically described as follows:
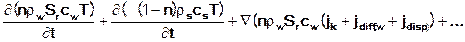
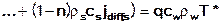
In this case, the right side of the equation presents the sum of all energy sources and sinks and T* the temperature of incoming and outgoing amounts.
In this equation, the mass fluxes for convection, dispersion and heat conduction are inserted. Using the product rule for the convective term and the continuity condition (see Mass transport ):
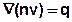
the transient energy equation results:
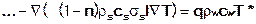
The heat diffusion parameters σw [m²/s] and σs [m²/s] are defined as:
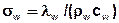
and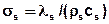 
Unit of the parameters:
ρw,s = density of the fluid (w) or the matrix (s) [kg/m³]
cw,s = specific heat capacity [J /(kg K)]
λw,s = heat conductivity [W / (m K)]
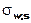= diffusion parameter = λw,s / (ρw,s cw,s) = [m²/s]
I = identity matrix [-]
D = dispersion tensor [m²/s]
Sr = saturation rate [-]
n = effective pore volume [-]
v = distance velocity [m/s]
q = div v (from continuity condition) [1/s]
T = temperature [K]
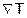= temperature gradient [K/m]
T* = variable temperature flow/discharge [K]
The energy transport equation and the heat production rate (QKON) have the unit [W/m³] = [J/(m³s)].
Boundary and initial conditions