Call via: Calculation 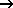Mass transport (density-dependent) appears the following input window:

 

When calling the module, the program reads the batch file with the default name (here: sitra.bsi).

 

Besides the already known input parameters „Stauts of Flow and Transport“ and „Time steps“ (see "Input parameters Mass transport“), in the density-dependent calculation the parameters for the change of density depending on the mass concentrations in the fluid are defined.

 

Iteration of saturation and density

The required number of iteration steps and the attenuation factor are determined.

 

Density parameters

Density ρ₀ of the reference concentration c₀ in [kg/m³]: ρ₀ = ρ(c = c₀), default is ρ₀ = 1000 kg/m³

Density gradient α = constant, default is α = 0.0

Reference concentration c₀ [kg/kg], default is c₀ = 0 kg/kg

The corresponding diagram can be represented and saved.

 

In general, the density ρ₀(c₀ = 0) of the reference concentration is known as well as the desired density ρ (c = C_max), C_max is typically the maximum concentration entered as 1KON or AKON.

With this the required density gradient α can be calculated by changing the linear density function that is programmed in the program module SITRA:

 

ρ(c) = ρ₀ + α(c - c₀)

to:

α = (ρ(c_max) - ρ₀) / (c_max - c₀), if c = c_max .

 

ρ₀ [kg/m³] = Density of the reference concentration c₀ = 0

ρ [kg/m³] = known/desired density ρ(c = c_max),

c₀ and c_max have to be entered in the unit kg/kg for the calculation of α .

 

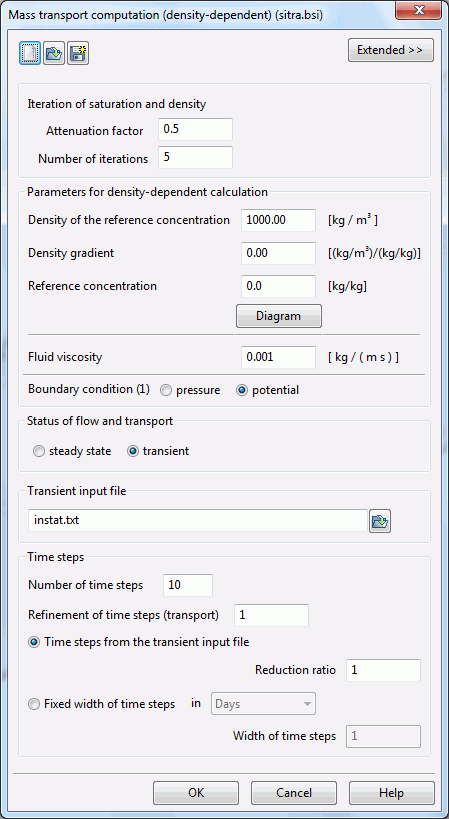
Numerical example for SPRING:

Density of the saltwater ρ(c) = 1021 kg/m³

Density of the fresh water ρ₀ = 997 kg/m³

Salt concentration c = 35 kg/m³,

For the calculation in SPRING the salt concentration c [kg/m³] has to be converted from the unit [kg/m³] into the unit [kg/kg]:

 

c_kg = c/1000 = 0,035 [kg/kg]

 

Substituting into the formula obtained:

α = (1021-997)/0,035 = 685,7 [(kg/m³)/(kg/kg)]

 

 

The corresponding density function looks like this:

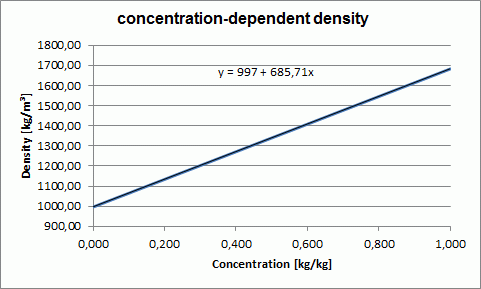
Density depending on the salt concentration in [kg/kg]

 

These numbers can be found in the sitr file in the 5th row:

4th parameter of row 5: ρ₀(c₀) = 997.0 (kg/m³)

5th parameter of row 5: c₀ = 0.0 (kg/kg)

6th parameter of row 5: α = 685.70 (kg/kg)/(kg/m³)

 

Specific density function for salt (sea water)

If the 5th and 6th parameter of the sitr file are set to -999.9, SITRA calculates with a specific density function for salt (T = 20 ° C):

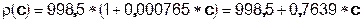
with:

ρ(c) = concentration-dependent density of the saltwater [kg/m³]

Density of the reference concentration (fresh water): ρ₀ = ρ(T=20°, c₀=0) = 998,5 [kg/m³]

Reference concentration: c = c₀ = 0 [kg/m³]

 

Regardless of the input for ρ₀ it is calculated with ρ₀ = 998,5 kg/m³.

 

 

General density function for salt

The concentration-dependent density function for salt water (sea water) is in general:

 

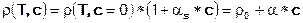
ρ(T, c=0) = ρ₀ = density of the reference concentration [kg/m³]

α_s: The factor α_s depends on the proportion and type of dissolved salts and is for sea water (see above) by a temperature of T = 20°C: α_s = 0,000765 [m³/kg]

c = Reference concentration [kg/m³]

α = density gradient, α = α_s * ρ₀ [-]

 

Fluid viscosity

The fluid viscosity (or dynamic viscosity) η (for water: η(T=20°) = 0.001 [kg/(m s)]) is needed, because in the density-dependent mass transport calculation the pressure equation is used.

 

Boundary Condition

While the density-dependent calculation, the input potentials or water levels (EICH, VORF, POTE) are internally converted in the unit pressure with the known formula:

 

If the water levels should be kept despite a change in density, the button "potential" (default) is enabled.

 

If the water levels should be corrected by the change in density, the button "pressure" has to be activated.

 

 

The buttons at the top of the input window allow resetting the input parameters (), opening an existing batch file () or saving the current batch file under another name ().

 

 

Extended