Bei der Gauß-Interpolation wird durch die vorliegenden Messwerte eine Interpolationsfunktion z(x, y) gelegt, die sich aus einer Linearkombination von Gauß'schen Glockenfunktionen für die Messpunkte zusammensetzt. Die Auswertung dieser Funktion in einem Interpolationspunkt liefert den Interpolationswert z für diesen Punkt.

 

Es seien n Messpunkte (x_i, y_i), i=1,...n, mit zugehörigen Messwerten z_i vorhanden.

 

Die Gauß'schen Glockenfunktionen (Grundfunktionen g_i) für die Messwerte sind Rotationsflächen mit ihrer Achse im zugeordneten Messpunkt (x_i, y_i):

 

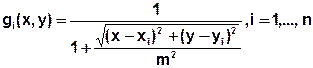
mit m: Mittel aller Messpunktabstände zueinander.

 

Die Grundfunktionen werden linear zu einer Flächenfunktion verknüpft:

 

z(x, y) = b₁ g₁(x, y) + b₂ g₂(x, y) + ... + b_n g_n(x, y)

 

Die zur Linearkombination verwendeten Koeffizienten b_j sind unbekannt und bilden die Scharparameter der Flächenfunktion. Die Bestimmung der Scharparameter ergibt sich aus der Forderung, dass die Messwerte auf der durch die Flächenfunktion definierten Fläche liegen müssen. Für jeden Messpunkt i ergibt sich eine Bedingungsgleichung:

 

z_i = z(x_i, y_i) = b₁ g₁(x_i, y_i) + b₂ g₂(x_i, y_i) + ... + b_n g_n(x_i, y_i)

 

Dies führt zu einem symmetrischen (n x n) Gleichungssystem für die n Unbekannten b_i , i=1,...n.

 

Nach der Ermittlung der Unbekannten b_i kann für jeden Netzknoten bzw. für jeden Elementmittelpunkt mit den Koordinaten x und y der zugehörige Funktionswert durch Einsetzen in die Flächenfunktion z(x,y) berechnet werden.

 

Um die Schwingungen in der Gauß'schen Flächenfunktion z (x, y) auszugleichen, wird diese noch mit einer weiteren Flächenfunktion

 

Z = Z(x, y) = B₁ g₁(x, y) + B₂ g₂(x, y) + ... + B_n g_n(x, y)

 

skaliert, deren Koeffizienten B_i , i = 1, ... ,n durch die Bedingung

 

Z_i = Z(x_i, y_i) = B₁ g₁(x_i, y_i) + B₂ g₂(x_i, y_i) + ... + B_n g_n(x_i, y_i) = 1 für i=1,..,n.

 

bestimmt werden.

 

Der Interpolationswert I in einem Punkt (x, y) errechnet sich damit zu

 

I(x, y)= z(x, y) / Z(x, y).

 

Implementierung in SPRING

Die Implementierung in SPRING nutzt Datenstrukturen und Parallelverarbeitung. Dadurch ist der Algorithmus extrem schnell und speicher-effizient. Das folgende Eingabefenster zeigt die Parameter für die Gauß-Interpolation:

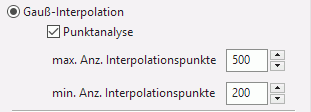
Gauß-Eingabe

Die wichtigsten Parameter dieser Methode sind die Anzahl der minimalen und maximalen Interpolationspunkte. Die Gauß-Interpolation erfordert mindestens zwei Datenpunkte. Je größer die minimale Anzahl ist, desto genauer ist das Ergebnis. Eine große Anzahl an minimalen Interpolationspunkten führt lediglich zu einem Anstieg der Rechenzeit, hat aber keinen großen Einfluss auf die Genauigkeit der Ergebnisse.

Die maximale Anzahl dient als obere Schranke für den Gleichungslöser. Im Übrigen lässt sich beobachten, dass eine annähernd gleiche Anzahl minimaler und maximaler Interpolationspunkte einen gewissen Genauigkeitsverlust zur Folge hat. Daher gilt als Faustregel, dass die maximale Anzahl der Interpolationspunkte etwa der 2 - 2,5-fachen Anzahl der minimalen Interpolationspunkte entsprechen sollte. Die Aktivierung der Checkbox "Punktanalyse" führt zu einem Zwei-Wege-Analysemodul, welches verschiedene Kriterien kontrolliert, um das bestmögliche Ergebnis zu erhalten. Da der Anstieg des Rechenaufwands durch Verwendung dieser Option im Vergleich zu den Hauptberechnungen vernachlässigbar ist, wird empfohlen, diese Option generell zu aktivieren.

Verschiedene Eingabeparameter führen natürlich zu unterschiedlichen Ergebnissen. Daher sollte großes Augenmerk auf passende Eingabeparameter gelegt werden, auch wenn der Algorithmus selbst so implementiert ist, dass nachteilige Auswirkungen durch unangemessene Eingaben weitgehend ausgeschlossen werden. Die Interpolation läuft vollständig parallel.

 

 

Flächeninterpolation