In the chapter "Steady state flow", the differential equation for a steady state flow with source and sink term is derived as a potential head equation and also as a pressure equation.

In the saturated, density-independent case, the transient flow equation is a function of the pressure:

 

 

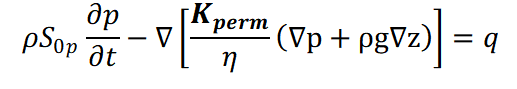
This means:

 

S₀ = spezific storage coefficient [1/m]

h = potential head [m], (sum of pressure- and potential height)

t = time [s]

K_perm = permeability [m²]

k_rel = scaling factor for the relative k-value [-]

η = dynamic viscosity [kg/(ms)]

ρ= density [kg/m³]

g = gravitational acceleration [m/s²]

z = alttitude [m]

p = pressure [N/m²],

q = sources/sinks term [1/s].

 

For the formulation of the transient pressure equation, the pressure-dependent specific storage coefficient S_0p is required, which is calculated from the effective porosity n of the aquifer, the matrix compressibility α and the fluid compressibility β:

 

S_Op = α(1-n) + βn

with:

S_0p = specific pressure storage coefficient [m²/N] = [ms²/kg]

n = effective porosity of the aquifer [-]

α = matrix compressibility [m²/N] = [ms²/kg]

β = fluid compressibility [m²/N] = [ms²/kg]

 

Note: If the compressibility of the entire system (attribute KOMP) is defined in the model file, the specific pressure storage coefficient (S_0p) is replaced by the total compressibility.

 

After including the density ρ, the specific pressure storage coefficient S_0p and a transient source/sink term – which is caused by density changes - the transient saturated/unsaturated density-independent flow equation is obtained as a function of the pressure:

 

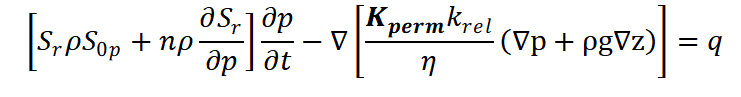
With:

S_r = S_r(p) = relative saturation as a function of pressure [-]

S_0p = specific pressure storage coefficient [m²/N] = [ms²/kg]

n = effective porosity of the aquifer [-]

 

In this case, the unit of the equation corresponds q = [kg/m³s]

 

Calculation of the storage coefficient