Für einen gesättigten Aquifer mit konstanter Dichte und stationärer Strömung lässt sich der gesamte Massenfluss j für den Stofftransport als Summe der einzelnen Massenflüsse aus Advektion (j_adv), Diffusion (j_diff) und Dispersion (j_disp) wie folgt mathematisch formulieren:

 

 

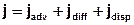
Da der Transport des Inhaltsstoffs nur im durchflusswirksamen Porenraum (n) des Grundwasserleiters stattfindet, muss dieser bei einer volumenbezogenen Betrachtung zusätzlich eingeführt werden:

 

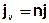
mit:

j_v = volumenbezogener gesamt Massenfluss [(m kg)/(s kg)]

n = durchflusswirksamer Porenraum [-]

j = gesamt Massenfluss [(m kg)/(s kg)]

 

Durch Einsetzen der einzelnen Komponenten, erhält man die Gleichung:

 

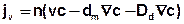
Der Anteil der molekularen Diffusion und die hydromechanische Dispersion können zur hydrodynamischen Dispersion zusammengefasst werden:

 

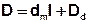
Mit der Einheitsmatrix I:

 

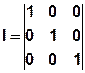
Es resultiert die Gleichung für den stationären Massenfluss:

 

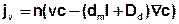
Die Massenbilanz ermöglicht die Betrachtung der Konzentrationsänderung über die Zeit (instationärer Stofftransport), bezogen auf die in ein Kontrollvolumen ein- bzw. ausfließenden Stoffmengen unter Berücksichtigung von Quellen und Senken (σ), d.h. Stellen, an denen dem System Stoff zugeführt bzw. entnommen wird:

 

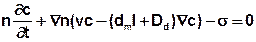
Der Term σ steht für alle Stoffein- und –austräge und kann folgendermaßen aufgeschlüsselt werden:

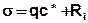
mit:

qc* = volumenbezogene Zugabe oder Entnahme von Wasser mit der Konzentration c*

R_i = Anteile aller nichtkonservativen Stofftransportprozesse wie Adsorption, chemische oder biologische Abbaureaktionen

 

Unter Anwendung der Produktregel für den Advektionsterm:

 

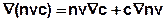
der Kontinuitätsbedingung

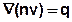
und der Zusammenfassung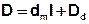

ergibt sich die instationäre Stofftransportgleichung für ideale Tracer bei konstanter Dichte des Aquifers zu:

 

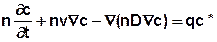
Beispiel:

q entspricht z.B. dem Attribut Knotenentnahme/-zugabe KNOT oder einer Reaktionsmenge, Einheit [m³/ZE] und c* entspricht dem dazu korrespondierenden Attribut KONZ.

 

Sind gesättigt/ungesättigte Verhältnisse im Aquifer vorhanden, muss die Sättigung S_r in der Stofftransportgleichung berücksichtigt werden:

 

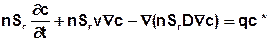
Die Einheit dieser Gleichung ergibt sich, abhängig von der Einheit der Konzentrationsrandbedingung, zu [kg Stoff / (kg Lösung *s)] oder [kg Stoff / (m³ Lösung *s)].

 

Behandlung nicht-konservativer Prozesse