In the chapter "steady state flow" the differential equation for a steady state flow with sources and sinks term is derived, as potential and as a pressure equation.

In the saturated, density independent case the transient flow equation as a function of pressure is formulated like this:

 

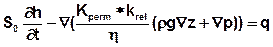
That means:

 

S₀ = spezific storage coefficient [1/m]

h = potential [m], (sum of pressure- and potential height)

t = time [s]

K_perm = permeability [m²]

k_rel = scaling factor of the relative k-value [-]

η = dynamic viscosity [kg/(ms)]

ρ= density [kg/m³]

g = gravity [m/s²]

z = layer height [m]

p = pressure [N/m²],

q = sources/sinks term [1/s].

 

 

 

The transient pressure flow equation requires the specific storativity S_0p. It depends on the flow effective porosity n of the aquifer, the matrix compressibility α and the fluid compressibility β.

with:

S_0p = specific pressure storage coefficient [m²/N] = [ms²/kg]

n = flow effective porosity of the aquifer [-]

α = matrix compressibility [m²/N] = [ms²/kg]

β = fluid compressibility [m²/N] = [ms²/kg]

 

Note: If the compressibility of the entire system (attribute KOMP) is defined in the model file, the specific pressure storage coefficient (S_0p) is substituted by the compressibility of the entire system.

 

After including the density ρ, the specific pressure storage coefficient S_0p and a - caused by changes of the density - transient source/sink term you get the transient saturated/unsaturated density-dependent flow equation as function of the pressure:

 

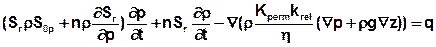
With:

S_r = S_r(p) = relative saturation depending on the pressure [-]

S_0p = specific pressure storage coefficient [m²/N] = [ms²/kg]

n = flow effective porosity of the aquifer [-]

 

The unit of the equation corresponds in this case to q = [kg/m³s]

 

 

Computation of the storage coefficient