The following input options appear:
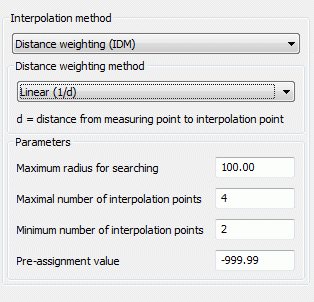
Input for distance weighting
The measured value is weighted depending on the distance d to the unknown node or element centre. For the weighting process, four different functions are available:
Based on Sampson (see in the following),
linear (1/d),
squared (1/d²),
4th degree (1/d4),
where d represents the distance between the measuring point and the interpolation point.
The user defines the maximum radius where measuring points are searched, the minimum and maximum number of measuring points used in each interpolation. If the defined radius does not contain enough measuring points, the value at the corresponding node or element is not interpolated. For these cases, the user defines a pre-assignment value.
Remark: In contrast, when interpolating data in the menu Attributes 
Assign By interpolation... nodes or elements for which were not enough interpolation points found get no value.
With the linear function, the influence of the measuring point decreases linearly with increasing distance. Having linear transitions between adjacent measuring points effects very rough interpolation areas. For a 4th-degree weighting, the influence of the point decreases with distance to the 4th power. Hence it follows that the value of the closest measuring point is the most significant one. The algorithm produces very smooth interpolation areas which are slightly graded around the measuring points. Squared weighting averages the two extreme values.
The algorithm based on SAMPSON (1978) was published as a “constrained distance-squared weighting”, and follows the weighting function
Compared to the other possibilities, this procedure delivers the best results.