This interpolation algorithm requires no additional input parameters.
In the first step of a Gauss interpolation, an interpolation function z(x, y) is fitted to the measured values. This interpolation function is a linear combination of Gaussian bell-shaped curves for the measuring points. The values of the function at the interpolation point obtain the interpolated value z at this point.
There are n measuring points (xi, yi), i=1,...n, with the corresponding measured values zi .
The interpolation function of a Gauss interpolation procedure is always based on the Gaussian normal distribution functions (fundamental form gi) for the measured values (xi, yi). They have the form
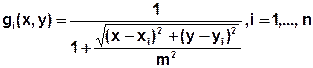
where m: average distance between all measuring points.
The fundamental functions gi represent surfaces of rotation whose axis of rotation is defined in the corresponding measuring point (xi, yi). They are linked linearly to a surface function:
z(x, y) = b1 g1(x, y) + b2 g2(x, y) + ... + bn gn(x, y)
The coefficients bj for the linear combination are unknown and represent the parameter of a family of the surface function. The measured values must lie on the defined surface. This leads to an equation for each measuring point i. With the help of this condition, the parameter of a family can be determined:
zi = z(xi, yi) = b1 g1(xi, yi) + b2 g2(xi, yi) + ... + bn gn(xi, yi)
Hence follows a symmetric (n x n) equation system for the n unknowns bi , i=1,...n.
The resulting values bi complete the surface function z(x, y). Substitution of the coordinates x and y returns the corresponding value at every node or rather element centre.
To prevent oscillations of the Gaussian surface function z(x,y), this is then scaled with an additional surface function.
Z = Z(x, y) = B1 g1(x, y) + B2 g2(x, y) + ... + Bn gn(x, y)
The coefficients Bi , i = 1, ... ,n are determined using
Zi = Z(xi, yi) = B1 g1(xi, yi) + B2 g2(xi, yi) + ... + Bn gn(xi, yi) = 1 for i=1,..,n.
bestimmt werden.
Finally, the interpolation value I at a given point (x, y) is defined as
I(x, y)= z(x, y) / Z(x, y).
Implementation in SPRING
The new implementation takes advantage of data structures and runs in parallel, making it quick and efficient in terms of resource management. Nonetheless, there are new parameters that should be chosen carefully to obtain the most appropriate results and performance. This section provides general guidelines on how to configure these parameters. The following figure shows the Gauss interpolation input window.

Gauß parameter
The most important parameters in this method are the minimum and maximum number of points. In general, the larger the minimum number of points, the smoother and more accurate the final results; however, it should be noted that using an unnecessarily large minimum number may increase calculation time without drastically affecting the results. On the other hand, the maximum number acts as a constraint and controls the behavior of the solver. Moreover, it is observed that a close minimum and maximum combination results in a slight decrease in performance. A rule of thumb would be to use a maximum number that is roughly 2-2.5x the minimum number. Furthermore, the point analysis checkbox invokes a two-pass analysis module that controls several criteria to ensure the best possible output is obtained. This option is found to enhance the final output in most cases; in addition, the increase in computational demand for using this option is negligible compared to the main calculations. Hence, it is recommended to keep this option enabled in general cases.
It should be clear that the mathematical model for the Gauss interpolation requires at least two data points.
Different input parameters will of course leas to different results, and especial care should be taken to use suitable input parameters; nonetheless, the algorithm has been implemented in a way to reduce any adverse effects stemmed from inappropriate input parameters as far as possible. Furthermore, this interpolation fully runs in parallel.

 Area interpolation
Area interpolation