The objective of inverse modelling is to minimize the target function. The target function consists of two main components:
ZF = ZFobs+ ZFpar
Both the measured values (ZFobs, i.e. potential heads, quantities) and the estimated values of the parameters (ZFpar, for example K-values, leakage coefficients, storage coefficients) enter into the target function. The shares are further divided
ZFobs = ZFPOTE + ZFLEAK + ZFKNOT
ZFpar = ZFKWER+ZFLERA + ZFKSPE
To determine the target function, a standard deviation 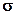 is assigned to each parameter and measured value. This corresponds to the expected error of the parameter.
is assigned to each parameter and measured value. This corresponds to the expected error of the parameter.
Each measurement value m, and each parameter value p is evaluated after each step of the inverse calibration as follows (method of type 'least squares’):
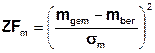
or 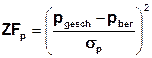
For the numerical solution of this nonlinear minimization problem, SPRING offers two different mathematical algorithms in the inverse modelling:

a Gauss-Newton-method by Levenberg-Marquard and

a gradient method by the Quasi-Newton-method
The shares of the target function of each measurement and of each parameter are summed. Chosing a small standard deviation 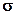 results in a large proportion of the target function and thus in a high weighting. From a large standard deviation
results in a large proportion of the target function and thus in a high weighting. From a large standard deviation 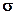 results a small proportion of the target function and thus a small weighting.
results a small proportion of the target function and thus a small weighting.
The following table shows the influence of weighting.
1.
2.
3.
4.
|
|
calculated |
measured |
Residual (calculated-measured) |
Standard dev. (Sigma) |
Proportion ZF (Residual²/sigma²) |
|
|
1. |
H1 |
65.285 |
66.040 |
-0.755 |
1 |
0.57 |
|
H2 |
66.985 |
66.230 |
0.755 |
0.1 |
57.0 |
|
|
2. |
Q1 [m³/d] |
-10000 |
-5000 |
-5000 |
1 |
25000000 |
|
Q2 [m³/d] |
-0.116 |
-0.058 |
-0.058 |
1 |
0.0033 |
|
|
3. |
Q1* [m³/d] |
-10000 |
-5000 |
-5000 |
500 |
100 |
|
Q2* [m³/d] |
-0.116 |
-0.058 |
-0.058 |
0.006 |
93 |
|
|
4. |
KWER [m/s] |
1.5e-3 |
1.0e-03 |
Log(1.5e-3)-log(1.e-3)=-0.699 |
0.3 |
5.43 |
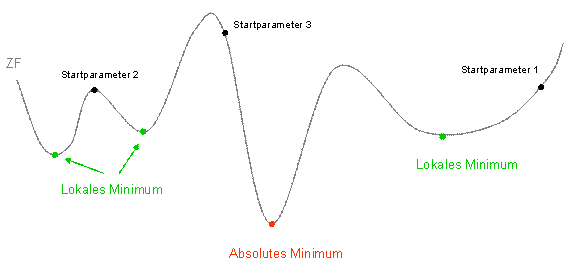
The following simplified illustration shows, why the initial values of the parameters can be crucial. The target function differs in size for different parameter values. There is an absolute minimum, as well as various local minima.
If you start the inverse modelling for example with the start parameter 1, the target function seeks to the associated local minimum. The target function for the start parameter 2 is on a local maximum and seeks to one of the two local minima.
The target function for the starting parameter 3 is at the highest, but the algorithm can reach the absolute minimum from this starting point. It is therefore quite reasonable to start the optimization process several times with different parameter values.
Formulation of the target function

 Realization in SPRING
Realization in SPRING