Ortsdiskretisierung bedeutet: Ein Untersuchungsgebiet wird in einzelne, geometrisch leicht erfassbare Teilbereiche zerlegt, für die mathematische Ansatzfunktionen definiert werden. Diese Teilbereiche mit den entsprechenden Ansatzfunktionen sind die finiten Elemente, die zur Vernetzung des Untersuchungsgebiets führen. Die Ansatzfunktionen werden durch so genannte Stützstellen, dies sind die Elementknoten, definiert.

Die Ansatzfunktionen, auch Formfunktionen genannt, sind Funktionen, die bei der Methode der finiten Elemente den realen Funktionsverlauf über dem Element bestmöglich annähern. Bedingung dabei ist die Erfüllung der Stetigkeitsbedingung. Da die Knotenpunkte von jeweils mindestens zwei Elementen geteilt werden, wird bei Verwendung der Werte in diesen Punkten die Stetigkeitsbedingung erfüllt. Der gesuchte Funktionsverlauf wird durch Interpolation der Werte in diesen Knotenpunkten näherungsweise bestimmt. Um den Funktionsverlauf u(x, y) durch die Knotenpunkte auszudrücken, verwendet man die Formfunktionen. Diese besitzen die Eigenschaft, im aktuellen Knoten stets 1 und in den restlichen Knoten 0 zu sein, so dass sich u(x, y) als Summe über die Anzahl der Knoten von u_i * N_i(x, y) ergibt, wobei i die Nummer des Knotens im Element und u den Wert am Knoten darstellt (abgeleitet aus Wikipedia).

Die lineare Formfunktion für das Einheitsdreieck mit den Koordinaten der drei Eckpunkte (0,0), (1,0), (0,1) sieht wie folgt aus (linearer Ansatz):

 

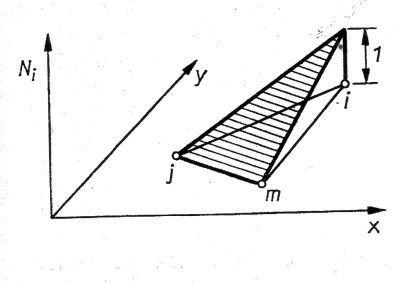
Lineare Ansatzfunktion für ein Dreieck

 

Für Viereckelemente muss ein bilinearer Ansatz verwendet werden, da die Kante eines Viereckelements mit einer Z-Koordinate ungleich 0 keine Gerade, sondern eine gebogene Linie darstellt (folgende Abbildung):

 

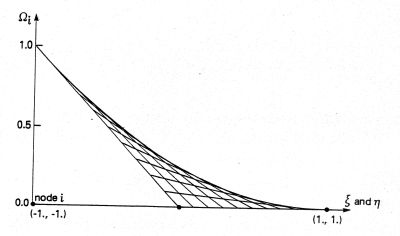
Bilineare Ansatzfunktion für ein Viereck

 

 

Noch deutlicher wird die Ansatzfunktion in folgender Abbildung:

 

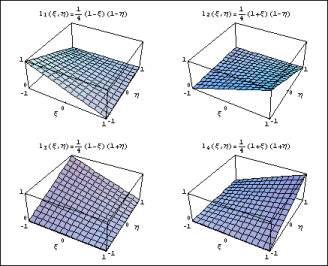
Bilineare Ansatzfunktion im Viereckelement

 

Umsetzung in SPRING