Viskosität
Die Viskosität ist eine Eigenschaft, die auf die innere Reibung der Flüssigkeit zurückzuführen ist. Die Einheit der Viskosität ist [kg/m s)] oder Pascal-Sekunde [Pa s].
Die dynamische Fluidviskosität η [kg/(m s)] und bei großen Temperaturgradienten die Dichte ρ [kg/m³] sind temperaturabhängige Größen, deren Veränderung mit der Temperatur zur Folge hat, dass die Differentialgleichungen (die instationäre Strömungs- und die Energietransportgleichung) ein gekoppeltes Differentialgleichungssystem darstellen! Eine experimentelle Formel zur Beschreibung der Beziehung zwischen dynamischer Fluidviskosität und Temperatur wird in der Berechnung verwendet:
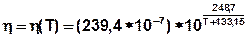
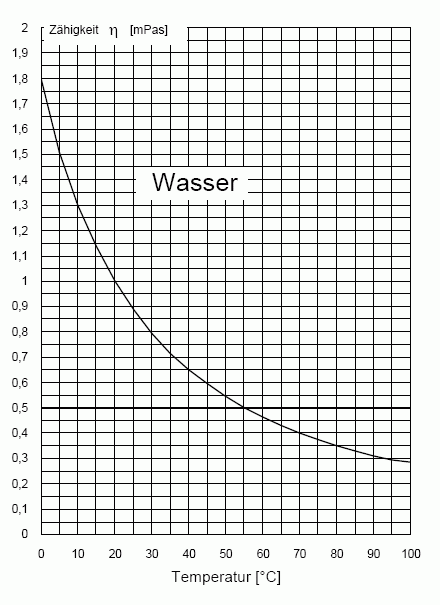
Dynamische Viskosität η des Wassers in Abhängigkeit der Temperatur bei einer Dichte von ρ= 1000.0 [kg/m³]
Die Einheit Millipascalsekunde [mPa s] entspricht der Einheit 1000*[kg/(m s)].
Es gilt folgende Beziehung zwischen dynamischer und kinematischer Viskosität:
Dynamische Viskosität: η = μ * ρ [kg/(m s)]
kinematische Viskosität: μ = η / ρ [m²/s]
mit:
η = dynamische Viskosität [kg/(m s)]
μ = kinematische Viskosität [m²/s]
ρ = Dichte [kg/m³]
Temperaturabhängige Dichte
In SPRING wird eine lineare Abhängigkeit der Dichte [kg/m³] von der Temperatur T [°C] berücksichtigt:
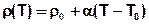
Mit:
ρ(T) = temperaturabhängige Dichte [kg/m³]
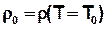
T0 = Referenztemperatur [°C], voreingestellt ist T0 = 20°C
α = konstante Dichtesteigung, voreingestellt ist α = 0.0
Die folgende Abbildung zeigt die Abhängigkeit der Dichte von der Temperatur:
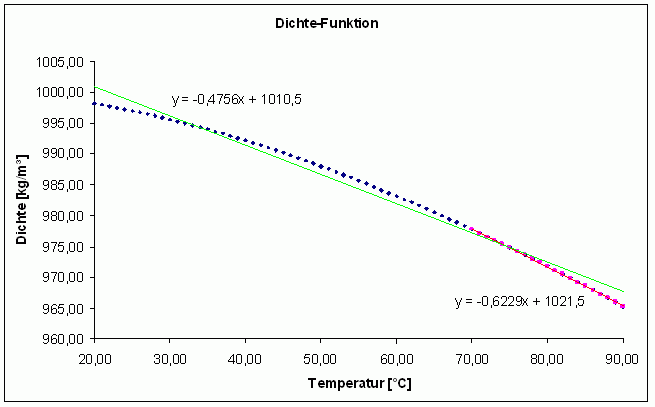
Temperaturabhängige Dichtefunktion
In diesem Fall ist:
ρ0 = ρ(T0=20 °C) = 1010,5 [kg/m³]
Die Dichtefunktion wird in dem zu betrachtenden Temperaturintervall (hier: ca. 32 - 75 °C) durch eine Geradengleichung (grüne Linie) angenähert, durch welche die Dichtesteigung α definiert wird.
Im Beispiel ist die Dichtesteigung α = konstant = -0,4756. (Dies entspricht der Steigung (= 1. Ableitung) der Geraden:
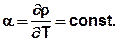
Liegen die Ausgangs- bzw. berechneten Temperaturen in einem anderen Temperaturbereich, so ist ggf. eine andere Ausgleichsgerade zu definieren (rote Linie).

 Umsetzung in SPRING
Umsetzung in SPRING