Bei dieser Vorgehensweise werden die ungesättigten Bereiche des Grundwasserleiters vollständig in die FE-Berechnung einbezogen. Die Strömungsgleichung wird in ihrer Form als Druckgleichung berücksichtigt. Für jeden Netzknoten wird aus dem aktuellen Druck p ein Sättigungsgrad S_r = S_r(p) berechnet. Für jedes Element wird dann aus den Sättigungswerten aller Eckknoten ein relativer K-Wert k_r = k_r(S_r) berechnet:

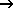Druck p_i Sättigung S_{r, i+1} und relativer K-Wert k_{r, i+1}

mit: i = Iterationsschritt

Um Oszillationen bei der Iteration zu vermeiden, wird die Änderung der relativen K-Werte von einem Iterationsschritt zum nächsten mit einem Dämpfungsfaktor 0< w < 1 versehen:

mit: i = Iterationsschritt

Bei w=1.0 wird die Iteration überhaupt nicht gedämpft, bei w=0. wird extrem gedämpft. Voreingestellt ist in der Regel ein Dämpfungsfaktor von w=0.5. Als Ausgangszustand für die Iteration werden wahlweise aus EICHpotentialen oder aus den Potentialen der null-Datei oder speziell über das Attribut ASAT (Anfangssättigung) berechnete relative K-Werte verwendet, oder die relativen K-Werte werden auf den Startwert = 1.0 gesetzt.

Innerhalb eines Iterationsschrittes wird der relative k-Wert so lange angepasst, bis die Unterschiede in den berechneten Potentialen zweier Schritte die vom Anwender eingegebene Iterationsschranke unterschreiten.

.

Anmerkung:

Bei der Iteration der freien Oberfläche können bei ungünstigen Modellparametern numerische Probleme auftreten, die im ungünstigsten Fall dazu führen, dass die Iteration nicht konvergiert.

Die Hauptursachen hierfür sind hohe Neubildungsraten für ungesättigte Bereiche. Die Iterationsverfahren neigen dann zu Oszillationen:

Sind die Elemente 'offen' (k = 1 bzw. k_r = 1), sinkt die freie Oberfläche unter die Lagehöhe der Elemente. Damit werden die Elemente im nächsten Iterationsschritt ungesättigt, also 'dicht' gemacht (k 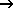0 bzw. k_r 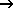0). Aufgrund der hohen Zuflussmenge bildet sich ein 'Potentialgebirge' auf diesen dichten Elementen, und die Elemente sind im nächsten Iterationsschritt wieder gesättigt, also 'offen' .

Durch eine starke Dämpfung, die allerdings auch die Konvergenzgeschwindigkeit verlangsamt und damit eine größere Anzahl Iterationen erforderlich macht, können diese Oszillationen in vielen Fällen vermieden werden.

Eingabeparameter