Im Kapitel “Stationäre Strömung“ wird die Differenzialgleichung für eine stationäre Strömung mit Quellen- und Senkenterm hergeleitet, als Potential- und auch als Druckgleichung.
Im gesättigten, dichteunabhängigen Fall lautet die instationäre Strömungsgleichung in Abhängigkeit des Drucks:
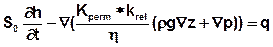
Darin bedeuten:
S0 = spezifischer Speicherkoeffizient [1/m]
h = Potential [m], (Summe aus Druck- und Potentialhöhe)
t = Zeit [s]
Kperm = Permeabilität [m²]
krel = Skalierungsfaktor für relativen k-Wert [-]
η = dynamische Viskosität [kg/(ms)]
ρ= Dichte [kg/m³]
g = Erdbeschleunigung [m/s²]
z = Lagehöhe [m]
p = Druck [N/m²],
q = Quellen/Senkenterm [1/s].
Für die Formulierung der instationären Druckgleichung wird der druckabhängige spezifische Speicherkoeffizient S0p benötigt, der sich aus der durchflusswirksamen Porosität n des Aquifers, der Matrixkompressibilität α und der Fluidkompressibilität β berechnet:
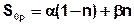
Mit:
S0p = spezifischer Druck-Speicherkoeffizient [m²/N] = [ms²/kg]
n = durchflusswirksame Porosität des Aquifers [-]
α = Matrixkompressibilität [m²/N] = [ms²/kg]
β = Fluidkompressibilität [m²/N] = [ms²/kg]
Anmerkung: Ist in der Modelldatei die Kompressibilität des Gesamtsystems (Attribut KOMP) definiert, wird der spezifische Druck-Speicherkoeffizient (S0p) durch die Gesamtkompressibilität ersetzt.
Nach Einbeziehen der Dichte ρ, des spezifischen Druck-Speicherkoeffizienten S0p und eines – durch Dichteänderungen bedingten – instationären Quellen-/Senkenterms erhält man die instationäre gesättigt/ungesättigte dichteabhängige Strömungsgleichung in Abhängigkeit des Drucks:
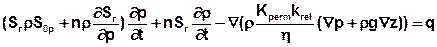
Mit:
Sr = Sr(p) = relative Sättigung in Abhängigkeit des Drucks [-]
S0p = spezifischer Druck-Speicherkoeffizient [m²/N] = [ms²/kg]
n = durchflusswirksame Porosität des Aquifers [-]
Die Einheit der Gleichung entspricht in diesem Fall q = [kg/(m³s)].
 Berechnung des Speicherkoeffizienten
Berechnung des Speicherkoeffizienten
